内部構造の発想
原因物から何段かの変形を経て、最終的に観測される表面的な特徴値に到るように、観測されるものには、その生成過程である内部構造が隠されていると考え
る。そして、その内部構造を明らかにしていくことが知的な認識であると考える。
初期の頃は、
下図のように、
一つの原像から何段かの変形を経ることによって形成される構造を考え、一つの原像から色々な形の観測値が生じる多様性を説明しよう
と考えた。
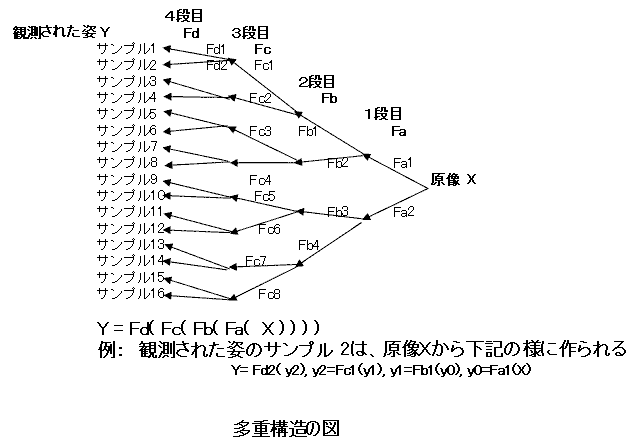
例えば、観測される特徴値を周波数スペクトルとすると、
歪んだ曲面をもつ鏡に像を写すように、周波数を高くしたり低くしたりする変形も必要となってくる。
そして、実際に、多段の変形からなる構造の方程式を解こうとすると、自由度が大きすぎて方程式が解けきれない、つまり、解の候補が多すぎて幾らでも都合の
良い解を求めることができ、そのままではパターン認識には使えないことが分かった。
(追記) キャラクター化された構造
何でも生成できる汎用的な構造に、内部の自由度に制限を加えて、生成できるものを限ることを考える。仮に、それをキャラクター化された構造と呼ぼう。キャ
ラクター化の種類は幾つかあるであろう。
入力されたサンプルを、そのキャラクター化された構造にあてはめて、無理やり解こうとしよう。その場合、そのキャラクター化された構造に上手く当てはまっ
てその構造から上手く生成できる世界と、うまくフィットしないでそのキャラクター化された構造では上手く生成できない世界に分かれるであろう。
構造の方程式を解く場合、自由度が多すぎると意味のある解が得られないが、キャラクター化された構造に分解し構成することで、この問題が回避できないか?
と考えている。
マッチングと学習
実際には、現実のサンプルに対して完全に形が一致する(完全再生)ように 構造からそのサンプルを再生することはできない。そこで、マッチングは、サンプ
ルにその構造(で再生できるもの、特徴)が(そのサンプルの一部分として)内在しているかどうかの判断になる。内在する構造の種類(キャラクター)が複数
あ
るときは、最終的には、これらの構造の組み合わせによるものになる。
学習は、多数のサンプルから、それらに共通に内在するコアである構造を推定することである。
多様性を減らす
次に、多様性を減らすため、音声の基本周波数(ピッチ)を基本波とした高調波成分の組を使うことを考えた。これならば、スペクトル上で周波数を高低の変形
に
よって生じる多様性から逃れることができる。

量子力学ちっくだが、観測量yとここでは音源に相当する原像xの間を結びつける、変形を意味する演算子Fがある仲間を作っているのではないかと考えてみ
た。
量子力学の世界では、演算子が群を構成する。仲間とは、群のようなものだ。量子力学の様な、数学的な対称性によって生じる奇麗な群とは おそらく おも
むきが違うことであろう。
特に、音声の場合、人間の口と舌と鼻の物理的な作りやその可動変形範囲による制限により、演算子Fのありようも有限個の仲間に制限されるものと推測され
る。
識別できるということは
世の中には、混沌とか曖昧で識別できないものと、また、識別できるものとが、存在する。そこで、識別できるものであるための条件が存在するだろう。
その必要条件を前提としてパターン認識の方法論を展開すれば、単純な一つの原理から色々と有益な式が出てくる複素関数論のように、有益な方法論が展開でき
ないだろ
うか、と思ったのである。
そのひとつとして、「相対的な相手同士がたがいに存在しあってこそ識別できる概念が成り立っている。」との仮説をたてて、それを同時存在性と呼んだ。
これまでのパターン認識の手法化のまとめ
アイデアの概念を実際に役立つようにするためには、それを数学的に扱えることが必要であろう。
キー
となる概念
|
数
学的に扱うための手法
|
同時存在性
|
とりうる値を有限な範囲に制限。 例:N値出力とか。
|
内部構造
|
構造式。 過去の生成経緯の、あらゆる蓄積。
|
構造の同定(推定)
|
細胞分裂のように、 はじめは粗く 段段 細かく 同定していく。
|
構造を推定する場合、一遍に、すべての定数を決め様とすると、あまりに自由度が大きいため、上手くいかないであろう。だから、大筋を割り振ることからは
じめ、じょじょに、細部をつめていく手法が考えられる。
しかし、一般論として、収束に要する時間と、必ずしも同じものに収束することが保証されない問題が残るであろう。
音声認識にあてはめるとしたら
それは、何かの音があるかないかの識別にはじまって、徐々に分化していき、最後に複雑な言葉の違いを使いこなすに至る、人類の進化の道をたどることに相
当する勉強かもしれない。
時間軸上の多様性から音素のキーとな
るもの
を見つけだす
通常の音声は時間の経過とともに変動する。そして、時間軸上で、特定の音素が、どこからどこまでと示す作業はあいまいであり、明確に区間することは難し
い。
そこで、時間的な変化のなかにも、音素を意味するキーとなる場所と、過渡的な変化中で生じた部分の2つの種類を考える。
そして、
(1)キー(となる場所)から次のキー(となる場所)への行き方は、一本道ではなく、多様な行き方が存在する。つまり、過渡的な場所はいくらでも変化する
ので
データベースをつくっても収束しない。
(2)キー(となる場所)とそれに行きつく近傍の部分を(内部)構造分析して、その構造にパターン認識のヒント(キーへの行き方)が隠されていないかどう
か探
るべきである。
のようなことを考えてみた。
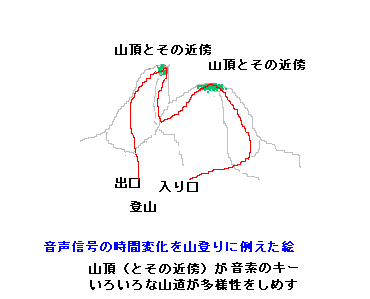
このことは、山登りに例えることができる。登山入り口から始まって、比較的緩やかな山頂をめざし、はじめの山の頂き(キーに相当)にのぼりつめた後、更
に、次に目指す山の間にある谷まで下降し、傾斜の厳しい断崖絶壁の側面を一気にのぼり、つぎの山の頂き(キーに相当)にとどりつき、そして、無事に、登山
出口へとおりていく。
登山入り口から山頂まで、山頂から山頂まで、山頂から登山出口まで、選択可能な複数の道が存在するだろう。これが、時間軸上の多様性である。しかし、キー
となる、山頂は、それぞれ1個しかない。また、ゆるやかとか絶壁などの山頂近傍の山の地形としての構造が、認識する上での何かのヒントになっているような
気がする。
No.13(J版) 2008年4月13日
格言:「科
学とは、扉をひとつ開けると、また、次の扉があらわれるようなものだ。」