< Chainerを使って 2次 IIR ノッチ フィルターを学習できるか? >
2次の IIR ノッチ フィルターの係数をChainerで学習できるかどうか試みる。
今一のフィット感しかない線形システムを (非線形要因も含むであろう)ディープラーニングを使って
より合致するようにチューニングできないか?と言うのが今回の動機である。しかし、
結論として、ニューラルネットワーク(RBM,LSTM,・・・)ではうまく学習できなかった。
その理由は、今回のようなノッチ型のデジタルフィルターを実現するには 連続的で微妙な計算精度が必要なこと、そして、
ニューラルネットワークが得意とする 内部状態が 非線形的に ざっくり 分離できるような対象になっていないため と考えられる。
結局、chainerを 過去とその過去の状態を記憶しておくRNN?構成にして、単なる”線形”の推定計算器としてもちいることにした。
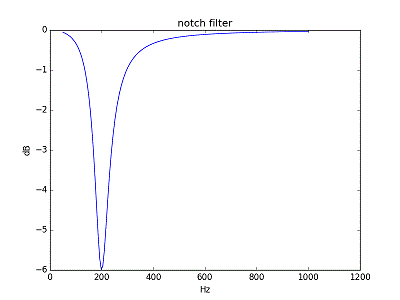
ノッチ フィルターの周波数特性の例を以下に示す。ノッチフィルターはある特定の周波数成分(ノイズなど)を除去する目的で使われる。
当初は、活性化関数を使うことを考えると出力の値が±1以内に収まる方がよい考え、信号が大きくなるブースト タイプでなく、信号が小さくなるノッチ タイプを用いることにした。
(デジタル)フィルターは以下の計算式で計算される。

上記の計算式の中の係数a[],b[]をノッチフィルターの場合 具体的に書いてみると
左列が減衰周波数が200Hzのもの、 右列が減衰周波数180Hzのものであり、小数点3桁目以降の微妙な差しかないことが分かる。
計算途中に活性化関数など 非線形にゆがめてしまうものが入ると フィルターそのものの再現が怪しくなる。
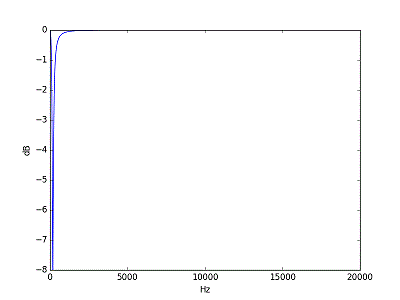
上図のノッチ フィルターの周波数特性の例は ある特性の周波数の部分を拡大したものであるが、
ナイキスト周波数の帯域からみると、下図の様に下線のゴミのようになってしまう。
SIN波を入力してSIN波を出力するニューラルネットワークは合成できるのであるが、このゴミのような微妙な周波数特性を学習できるようにはできなかった。
chainerを 過去とその過去の状態を記憶しておくRNN?構成にして、単なる”線形”の推定計算器として使うことにした。
これでは、他の数値計算手法と変わらないので わざわざchainerを使う必要はないのであるが、やってみることにした。
ネットワークの構成を class CharRNNとして以下のように定義した。

h2,h3,h4,h5が入力と出力それぞれの過去とその過去の状態を記憶することを意味し、forward_one_stepは(デジタル)フィルターの計算式に倣っている(以下の表も参照のこと)。
前述の理由から活性化関数(tanh,・・・)はコメント文にして使っていない。
推定計算を実際に行ってみると、初期値>0の場合、直流が加算しているようなもので、そのうちにバイアス要素は零へ収束していくことが分かる。
そこで、Linearのオプションでnobias=Trueを指定して はじめからバイアス無しにしている。
optimizer ADAMのステップ毎にパラメーターを更新する大きさアルファの値も、デフォルトの値より1桁小さくした。微妙な変化しかない超平面上を
うろつくので大きすぎると行き過ぎて収束しないようである。

下記の表は、フィルターの係数とCharRNNの中のパラメーターとの対応を示したものである。
2次のIIRフィルターの係数a[],b[]は6個あるが、ノッチフィルターはそのうちの3個だけを使って実現できる。
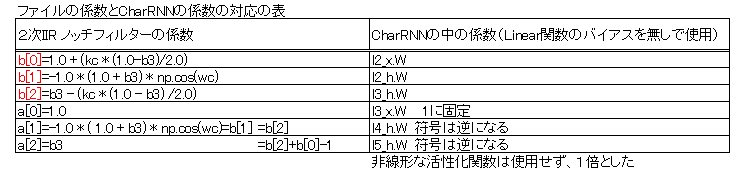
係数を束縛してこの3個だけを使えば ネットワークが ノッチ型の周波数特性をもつことは(値が正ならば)保証されるはずであるが、自由度を拡張して 4個、5個にした場合の結果も最後方に示しておく。
今回の課題は
初期値 initial
減衰周波数200Hz
減衰利得-6dB
Q(減衰する周波数の幅に相当)8
の2次 IIR ノッチフィルター からスタートして
目標 target
減衰周波数180Hz
減衰利得-8dB
Q(減衰する周波数の幅に相当)8
の訓練データを与えた学習調整後の値 present
が目標にどれだけ近づけるか?
下図は 初期値、目標、学習調整後、それぞれの周波数特性の比較例である。
減衰周波数は目標に達しているが、減衰利得や幅は外れている。
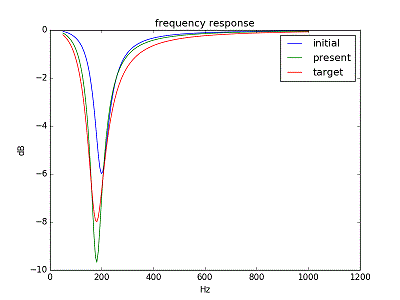
ネットワークのパラメータは乱数で初期化されるが、ここでは対象の素性はおよそわかっている場合を想定し、
乱数ではなく上記のように具体的な値を初期値として与えいる。
訓練は、異なる5個の周波数帯域の中から それぞれランダム選んだ周波数をもつSIN波の入出力信号を使っておこなった。
異なる5個の帯域が同時?に成り立つような、連立方程式を解くような効果を期待している。
ナイキスト周波数からみると減衰する周波数帯域はごく狭い範囲のため、均等に分割してしまうとその特徴は埋もれてしまう。
入力に一様乱数をつかう場合でも、このように狭い特徴の学習は難しい。
そこで、特徴を表す部分をクローズアップした、以下の6個の周波数で区切られた周波数帯域(BAND)を使用した。
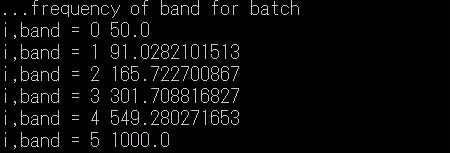
下図は、1帯域(1バンド)あたり 500サンプル分の 正規のIIRフィrターで計算したものと訓練学習したRNN?ネットワーク出力の比較例である。
1から500までは初めのバンド、501から1000までが次のバンド、更に次は1001 から1500までと、合計5バンド分2500個を表示している
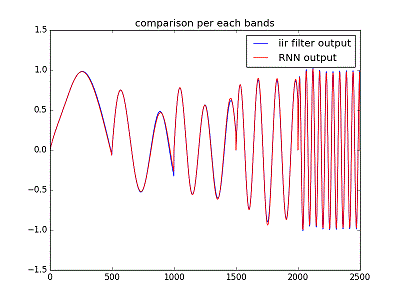
ネットワークのパラメータの更新は、5帯域(5バンド)の シーケンス長 500サンプル毎に行う。
損失は、正規のIIRフィrターで計算したものと 訓練学習したRNN?ネットワーク出力 の差の 二乗平均で評価した。
下図は、パラメーター更新回数とその損失(ロス)の変化の様子。
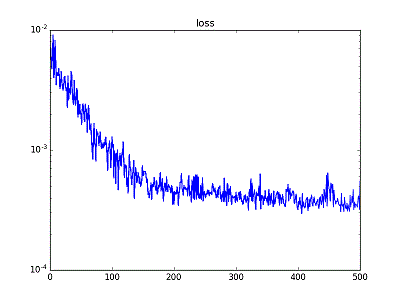
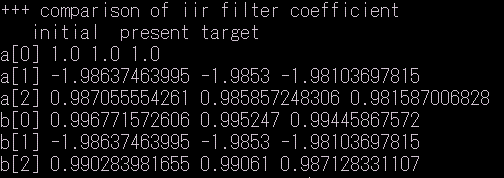
初期値、学習調整後の、目標値、それぞれのフィルターの係数a[],b[]の値。

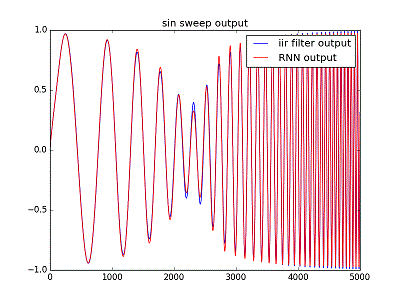
下図は、入力信号に 低い周波数から高い周波数まで連続的に周波数を変化(スイープ)させたSIN波を使ったものの比較で、減衰周波数付近で振幅が減衰することが分かる。
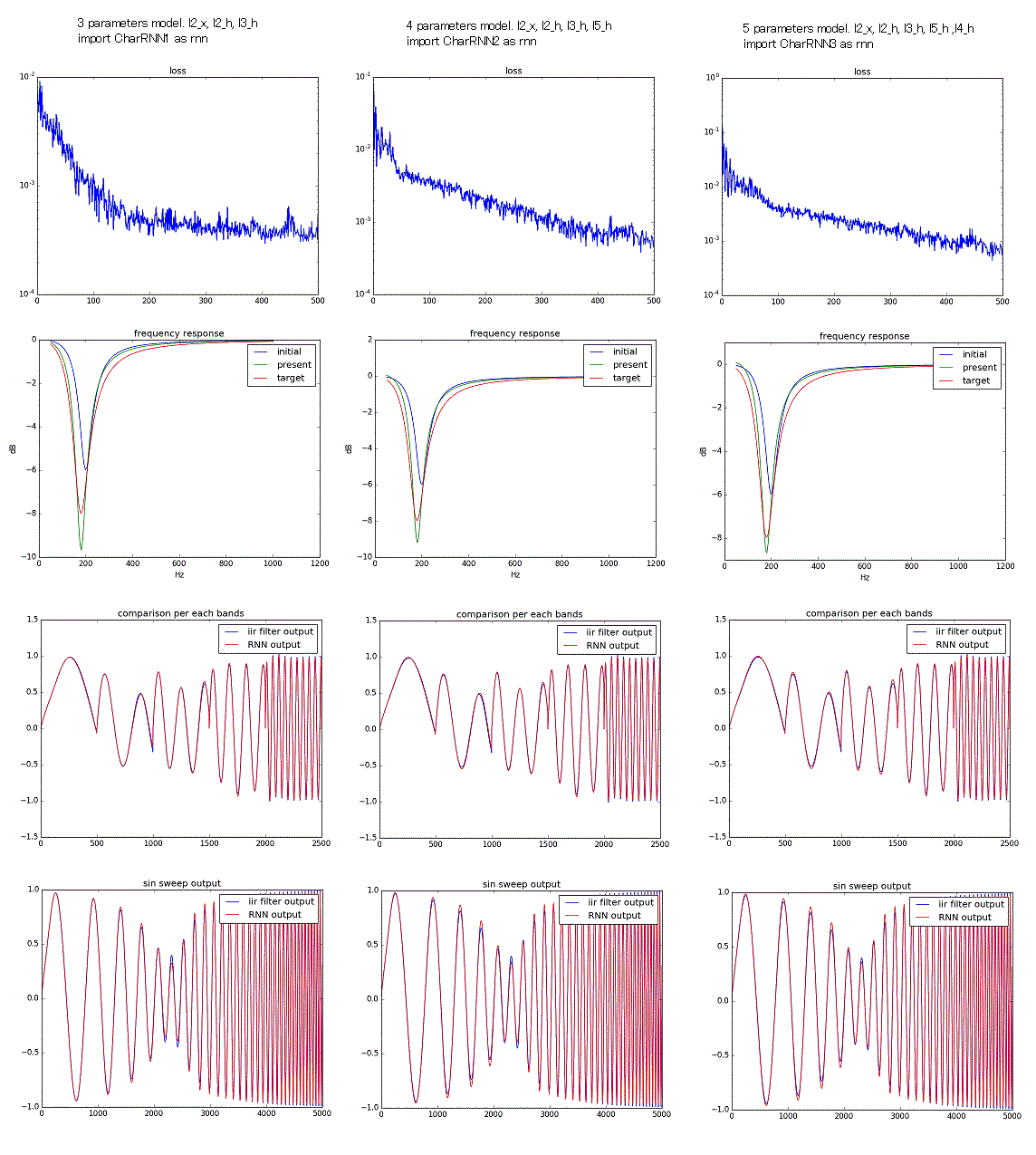
以下は、自由度3個、4個、5個の場合の結果の比較である。
作成したプログラム(python2) (以前のプログラム)













