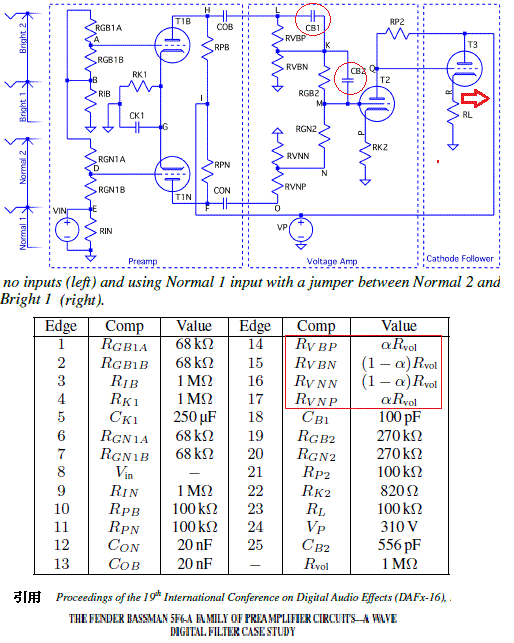
Wave Digital Filter

　電子回路をコンピューター上で高速に（できれば実時間内で）計算する手法として　Wave Digital Filter　と呼ばれる手法があるが、日本語の解説文献がほとんどない。
電子部品のV-I特性（キルヒホップの法則）を、入射波と反射波の入出口をそなえたポート インピーダンスの部品？に置き換えることらしい。
　ポート インピーダンスを適切な値に置き換えることにより、反射波を　過去または現在の入射波からのみで計算できるようにすることができて、回路を逐次的に計算することが可能となる（つまり　入射波と反射波を同時に連立して解く必要がなくなる）。これが　Wave Digital Filter　を導入するミソのよだ。部品の特性を入射波と反射波を使ってサンプリング時間毎の逐次計算に置き換えるので、多分、　波形　デジタル化　フィルター　Wave Digital Filter　と呼ばれる理由であろう。
2ポート部品？の並列または直列の組み合わせだけで、すべての回路を　反射波を　過去または現在の入射波からのみで計算できるように変換することはできない。そこで、複数の入射波と反射波の入出口（6ポート以上？）をもつ（複雑な内部配線をもった）部品？を使うことで、反射波を　過去または現在の入射波からのみで計算する方法がある（R　タイプ　アダプター）。
一般的に、真空管やダイオードなどの非直線素子の場合は、入射波と反射波を直接計算するのは難しい。そこで、通常のV-I特性をニュートン法などの逐次計算で求めてから、入射波と反射波へ　サンプリング時間毎に変換する。非線形に起因する高調波の影響を少なくするため、サンプリング周波数を高くして計算するのが一般的のようだ。例えば、真空管モデルではサンプリング周波数を4倍にした入力信号を使っているようだ。


■Wave Digital Filterの参考資料　-どれも英文で難解なものが多い-


■Wave Digital Filterのライブラリーソフト -真空管プリアンプの回路JTM45をRT-WDFで計算してみた。


■Wave Digital Filterではないが　実時間処理を目指したソフトや論文


(追記） ■rt-wdfとLTspiceの比較

下図の様な、2段の真空管　増幅回路と　出力トランス（等価回路）からなるシュミレーションを行ってみた。
Ayumiさんが公開している資料を使って6K6(の3極管おきかえ）と、OPT2K5のトランスデータを使って、モデルを作成した。
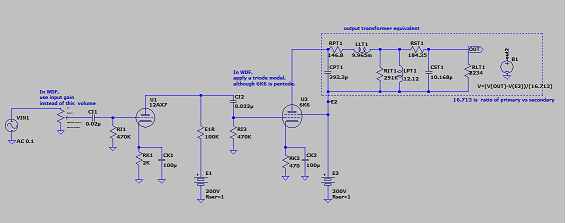
Two_Triode_Amp_Circuit-smal

作成時間はかかるがLTspiceで作った方が音がよい。真空管回路の音の比較では、4倍の17600Hzより等倍の44100Hzの方がよい気がする、サンプリングレートコンバーターの影響もあるかもしれない。
RT-WDFで音を作成するためには、S,E,F,M,N行列を計算して、ビルドしなくてはならないのは、かなり手間のかかる作業だ。計算時間がかかってもよいならば、LTspiceを使った方が便利だ。
理想?部品のシュミレーションでは、真空管の熱さやトランスの個性など　音の違いは、表現できない。


参考にしたもの

(さらに追記）■12AX7差動入力の2A3プッシュプルパワーアンプ

12AX7差動入力の2A3プッシュプルアンプをwave digital filterを使って合成してみた。

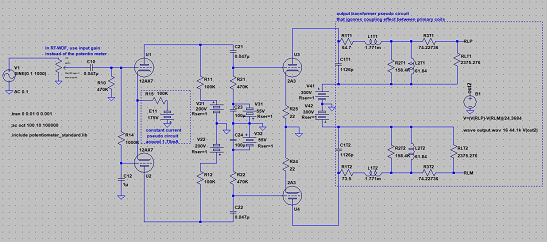
Triode_Sadou_PushPull_Amp_Circuit-small

初段は、定電流回路を疑似的に電圧源で置き換えたものを使った差動アンプ。
終段は、出力トランスを2個並べて数学的に加算することで実現した？　真空管のプッシュプル回路。
初段の電圧増幅には12AX7、終段の電力増幅には2A3相当のモデルを使っている。（特性は本物に似せたもので、別ものである）
  1. 定電流：疑似的に 電流源を電圧源＋シリーズ抵抗に置き換える方法で合成した。電圧源置き換え方式では、完全な固定電流にならず負荷に応じて少し電流が変動する。
  2. 数字的に同じ特性の真空管を2個並べている（完全なマッチドペア）が、差動の出力の動作ポイントがずれてしまう。 rt-wdfのオリジナルのtriodeモデルでは、Ig0　ゲート電圧が負の時に流れる最小のゲート電流が有限なため、入力側にオフセットが発生しているためと判明。 Ig0を零に変更した。
  3. プッシュプル用に出力トランスは　入力側に2個の巻き線、出力側に１巻き線あり、3個の巻き線が相互に磁気結合している。 3個の巻き線のトランスの等価回路もあるらしいが（かなり複雑!）、ここでは単純に出力トランスを2個並べて、出力側の電圧を数学的に加算することで プッシュプル回路を実現？することにした。 入力側の2個の巻き線間の磁気結合は無視することになる。2A3の出力インピーダンスは800Ωと小さめなので、入力側の巻き線間の磁気結合の影響は小さいであろと希望的観測をしている。
  4. 2A3は直熱管であるが、カソードを小さい抵抗（ヒーター巻き線相当？）を経由してGNDに落としてある。（実際にはトランスのヒーター巻き線（センタータップがＧＮＤ）につながる）、ゲート側に-55Vのバイアスを掛けている。
  5. rt-wdfで計算した出力の値が途中から零に落ち込んでしまう問題があり。かなり悩んだが、原因は、非線形の素子（ここでは真空管）の値を ニュートン法の反復計算をしている箇所で、Ｆ行列?のノルムに異常が発生していることと判明（下図）。
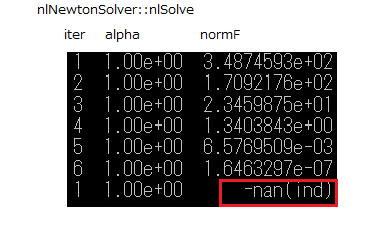
    normF error
    対策として、反復ステップの係数alphaを小さくすることにした。 （小さくする分、反復数が増して時間が掛かるデメリットがある。）
  6. 計算出力をWAVファイルで変換するとき、１Vがフルビット相当なので、WAV変換で信号がクリップしないように出力電圧が小さめにボリュームを調整している。（JUCE上で入出力ボリュームは設定変更可能）
  7. 真空管12AX7と2A3,出力トランス(F2021)は、Ayumiさんが公開しているデータからrt-wdf向けのモデルを合成した。

上記のように差動回路出力とプッシュプル回路入力をコンデンサーでC結合せず、計算上で差動出力の電圧値を直接プッシュプルの入力に入れた 方が（下図の回路図）、音（おと）的にはよい印象を得た。プッシュプルと差動部分の干渉がなくなるためか、高域の周波数特性も改善している。もとのC結合だと、20KHｚの減衰が少し大きい。

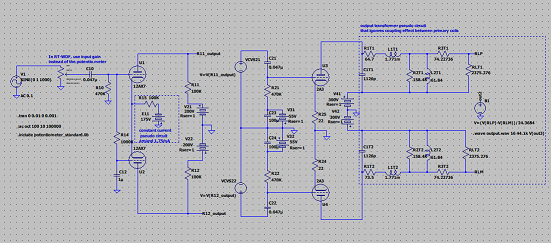
Triode_Sadou_PushPull_VCVS-connect_Amp_Circuit-small

ここでのVCVSは、Voltage Control Voltage Sourceの意味で、差動回路の出力をそのままミラーして出すだけである。
動作は不安定ですが、実験用に作ったものです。


（その他）
音質と高調波の関係は謎が多いようだが、下記が参考になりそうだ。

1KHzの-10dBのsin波を入力して、真空管アンプのシュミレーション回路の2倍（偶数次高調波）と3倍（奇数次高調波）の発生の様子を見てみた。

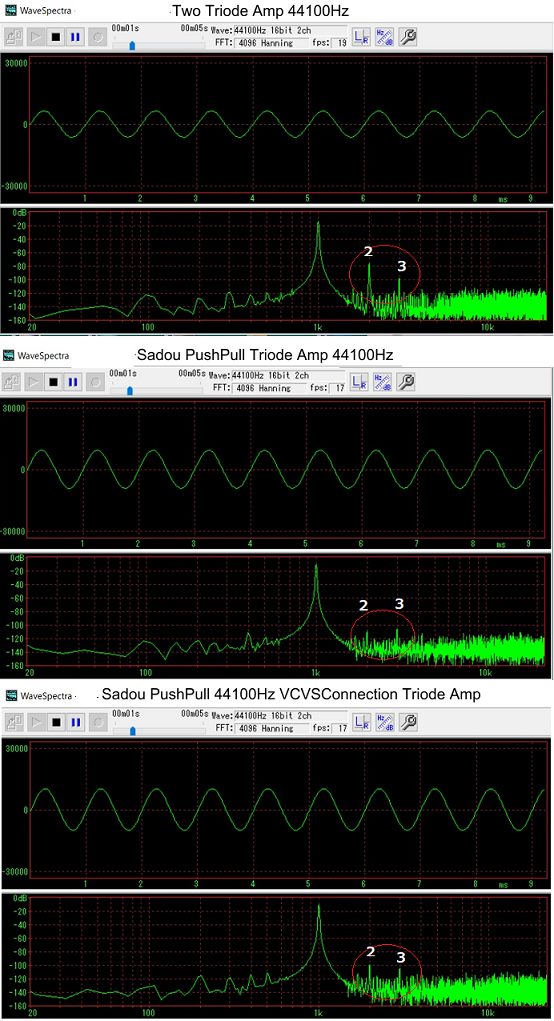
baion

単純な2段アンプ回路(Two Triode Amp)では2倍3倍の高調波はともにそこそこ出ているが、 差動プッシュプル回路(Sadou PushPull Triode)ではかなり減っている。
更に、前段と後段のつなぎを理想VCVSに変更すると(Sadou PushPull VCVS connection)　2倍（偶数次高調波）の方が3倍（奇数次高調波）より大きくなっていた。-90dB程度とかなりレベルが低い違いなのに、音質に違いがあるのは不思議だ。

■免責
(1)回路図やプログラムやデータの使用により、使用者に損失が生じたとしても、その責任 を負いません。
(2)回路図やプログラムやデータにバグや欠陥があったとしても、修正や改良の義務を負い ません。