| Min |
Typ |
Max |
|
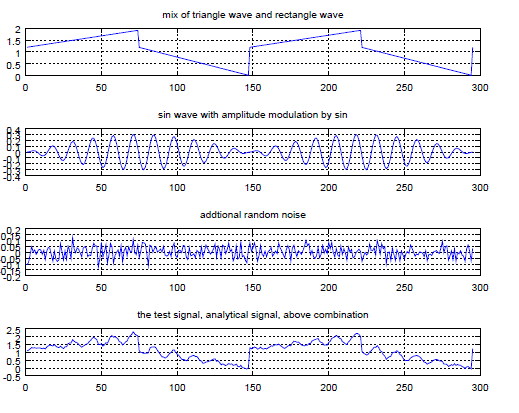
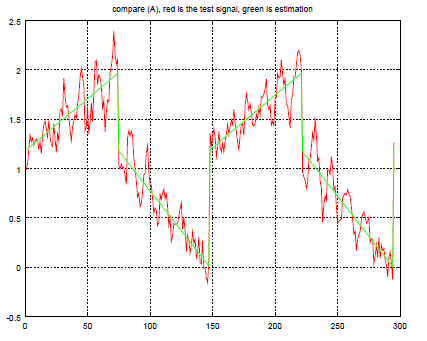
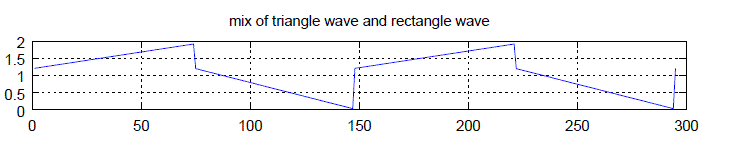
| Structure A, frequency, f0 |
100 |
550 |
1000 |
| Structure A, amplitude value, height0 |
0.1 |
1.05 |
2.0 |
| Structure A, ratio of triangle signal to rectangular signal, ratio0 |
0.5 |
0.7 |
0.9 |
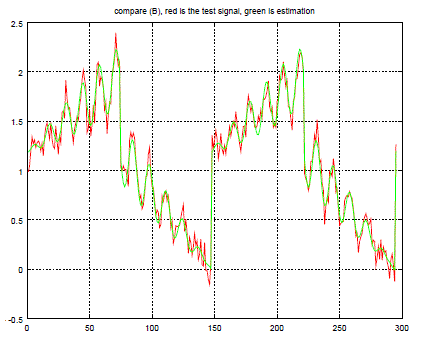
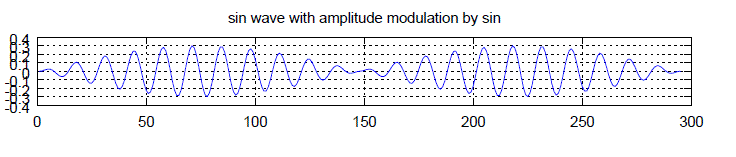
| Structure B, frequency, f0 |
100 |
550 |
1000 |
| Structure B, amplitude value, height0 |
0.1 |
0.55 |
1.0 |
| Structure B, ratio of carrier frequency to amplitude modulation frequency, ratio0 |
8 |
10 |
12 |