>
<フォルマント周波数の比は近似的に不変量か?>
〔命題〕 音声の母音のフォルマント周波数の比は、近似的に不変量になっているのか?
話す人が異なっても、母音をその音として認識できるので、音の中になんらかの共通の不変量?が存在するのではないかと考える。話す人によってフォルマント周波数そのものは異なるので、不変量の候補として、フォルマント周波数の比を考えてみよう。
更にいくつかの補足仮説を立ててみる。
①人の聴覚は周波数が高くなるほど、周波数分解能が低下していくので、第1フォルマント、第2フォルマント・・・などの 周波数が低い順の、比較的低次のフォルマントの周波数の比率が重要である。
②発声器官は大まかには同じ構造をしているが、大きさや細部の形状については個人差があるので、おおよその範囲内の値をとる つまり 近似的な不変量となるだろう。
③フォルマントの比 以外の複数の要因から音を判定しているため、実際に許容される フォルマント周波数の範囲は限定される。
④フォルマント周波数の振幅(強さ)は音声の伝送経路の環境によっても変わるので、振幅の絶対値そのものが不変量にはなりにくい。
さて、下図のような、第1フォルマント周波数を1として 周波数特性を定義しなおした、正規化周波数を導入しよう。周波数の絶対値が異なっていても周波数の比が保たれているということは、正規化周波数でピークの位置が同じことと同等である。
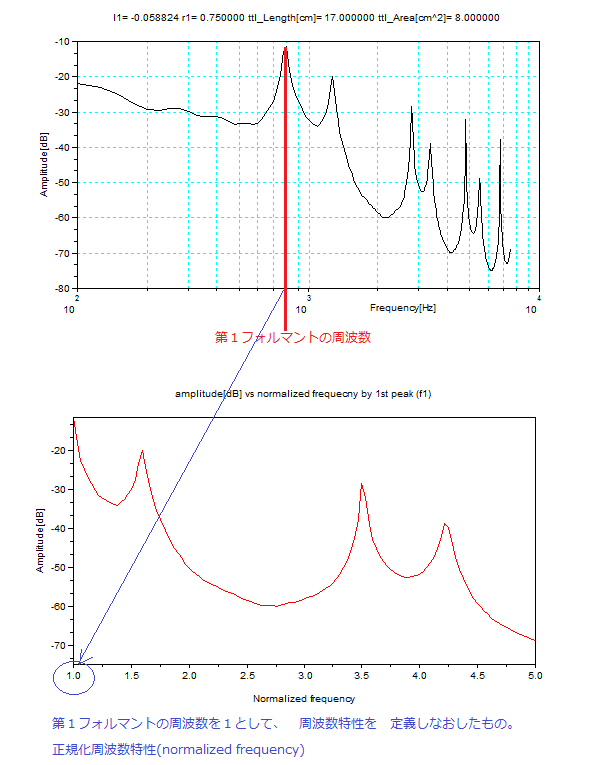
正規化周波数のピークの位置をほぼ保ったまま、発声モデルを簡略した2管声道モデルをつかって、3種類の音を合成してみた。
下図は、周波数特性、正規化周波数特性、2管声道モデルの形状を示す。左側から 声道の大きさとして、中、小、大の順番で並んでいる。母音を変えないため2管声道モデルの長さ比率(l1)と面積比率(r1)は
変えないで、小は 中より声道の全長(ttl_Length)や全面積(ttl_Area)を小さくしている。 小は、管が小さくなって反射時間が短く
なるので 中より 周波数の絶対値が 高くなっている。 逆に、大は周波数が低くなっている。いずれの場合も、正規化周波数上のピークの位置はほぼ同じに
保たれている。
母音/a/の例:
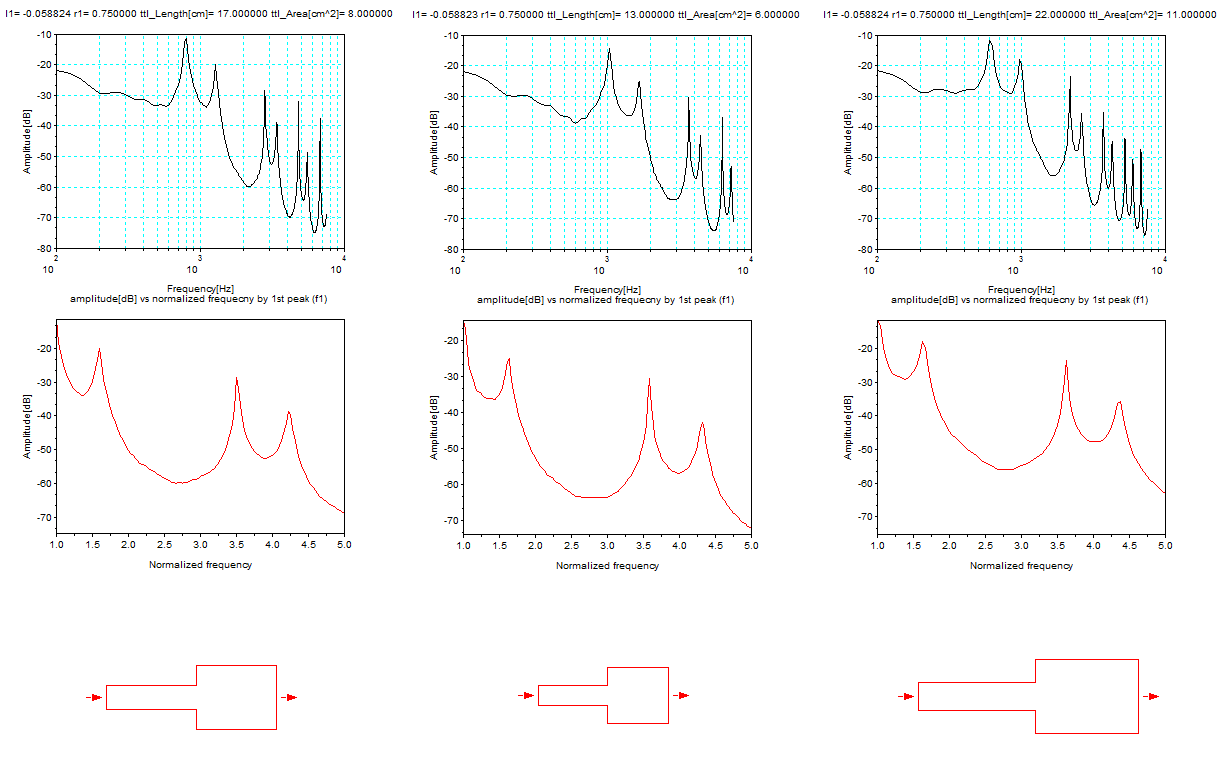
合成した音(WAVファイル) /a/
y3out_xmode6_Lng17_Ara8.wav y3out_xmode6_Lng13_Ara6.wav y3out_xmode6_Lng22_Ar11.wav
2管声道モデルの音質はよくないが、左端の1番目(声道の大きさ中) のWAVファイルを再生してみると「あ」と聞こえる。 2番目、3番目と、長さや面積を変更していくと、だんだん、明瞭度が悪化していく。更に、長さを短く面積を小さくしていくと、ブザー音の様になる。
母音/ae/の例:
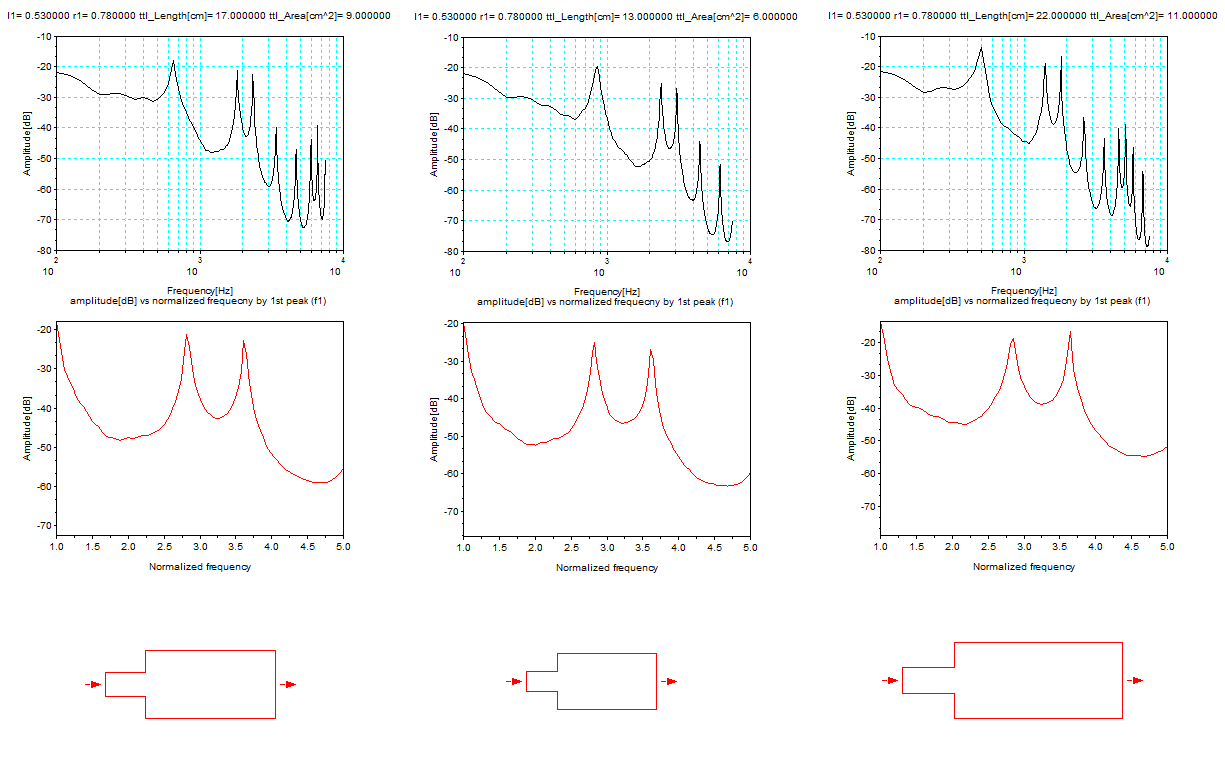
合成した音(WAVファイル) /ae/
y3out_xmode7_Lng17_Ara9.wav y3out_xmode7_Lng13_Ara6.wav y3out_xmode7_Lng22_Ar11.wav
WAVファイルを再生してみると、「え」と聞こえる。
フォルマント周波数の比を保ったまま 周波数の異なる音サンプルを合成して母音が保たれるかどうか試してみたが、、
これだけでは、命題を肯定するには不十分ではある。
上図を作成し合成音を作ったSCILABのプログラムもリンクしておきます。
No.2b 2015年9月25日


