音声のバンド・パス・フィルター・バンクによる分析とその応用

バンド・パス・フィルター・バンクとは、通過周波数の中心値が少しずつ違う複数の帯域通過フィルター（以下、ＢＰＦと呼ぶ）を複数個　並列に並べたものである。２ＫＨｚを超える周波数成分の状態を調べるため、音声のバンド・パス・フィルター・バンクの出力を、グレーススケールの画像で可視化する。
また、応用として、音源のノイズの状態をガウス分布に当てはめて、共鳴の強さを求める。
２管声道モデルに当てはめ、声道の状態を断面積と長さで近似する。

音声のバンド・パス・フィルター・バンクの出力

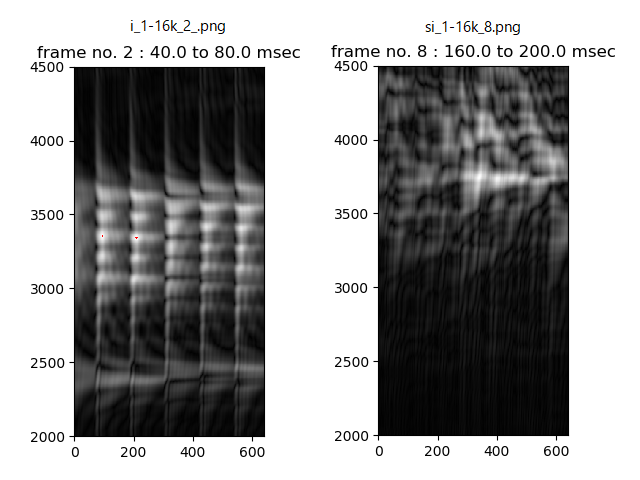
下図は、通過周波数の中心値が２０００から４５００Ｈｚの間で５Ｈｚ毎のＢＰＦの出力波形の包絡線（絶対値）をグレースケールの画像で可視化したものである。入力信号は、Ｆ０やＦ１などの低い周波数成分の影響を除くため、８００Ｈｚのハイパスフィルターを掛ける前処理をしている。
左側は単独で発声した母音の「い」の部分を、右側は摩擦音の「し」のはじめの子音の部分をグレースケールで画像化した例である。
母音「い」では、周波数軸上にも時間軸上にも周期的な強弱（白黒）がみられる。時間的な強弱はピッチ（基本周波数Ｆ０）の影響である。周波数上の強弱は口腔内の共鳴（フォルマントＦ２，Ｆ３）の影響と考えられる。
摩擦音の「し」の子音部分では、３ＫＨｚを超える信号がなだらかに発生していることが分かる。

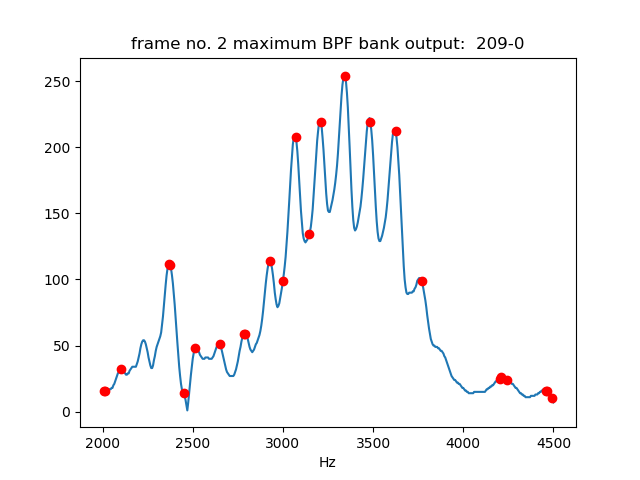
母音の「い」の例で、分析したフレーム内で最大の値を持つ箇所を中心に詳しく見てみよう。（左側のグレースケール画像の中で、値が２５０超える、強い箇所を赤くしてある。）
下図は、周波数特性である。３３４０Ｈｚを中心とする山形の大きなスペクトルと、複数の鋭いピークが存在することが分かる。（グレースケールのため値は０～２５５になっている。）

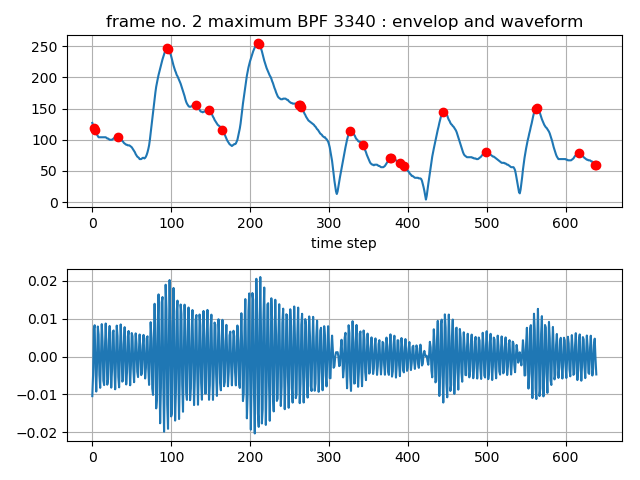
下図は、通過周波数の中心が３３４０ＨｚのＢＰＦの時間軸上の出力波形である。ピッチに同期したバースト状の波形になっている。

上図に見られる３３４０Ｈｚを中心とする山形の大きなスペクトルが、声門のパルス音源に起因するものか、別の乱流音源に起因するものを考察する。
一般に、波形が一定でない形状（ここではバースト状）になることにより、見かけ上スペクトルが広がる（スペクトルリーク）。予想されるスペクトルリークより明らかに広い帯域の信号が発生していれば、乱流音源（ノイズ性の音源）が発生している可能性が考えられる。
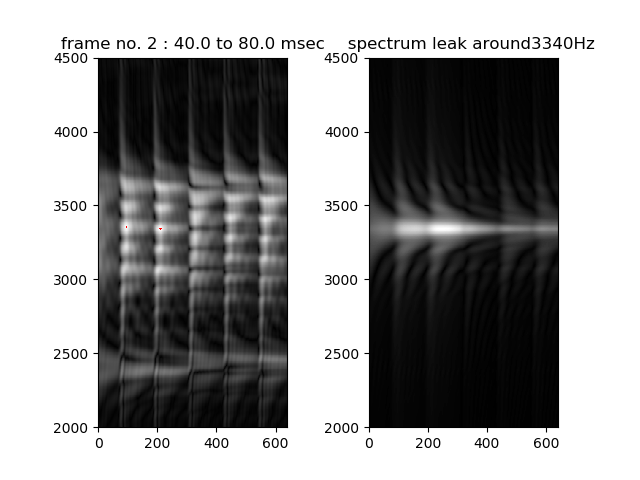
下図は、左側が形状のもととなる音声の出力で、右側は同じバースト状の波形をもつ純粋なＳＩＮ波（ここでは３３４０Ｈｚ）のスペクトルリークを計算したものである。フォルマントＦ２とＦ３の２つの信号のスペクトルリークだけでは帯域が広いことを説明するのは難しいので、乱流音源も発生していた可能性が考えられる。

ノイズ性の音源の分布の推定と共鳴の強さ

口腔内でノイズ性の音源（乱流音源）が発生し、口腔内の共鳴である特定の信号が増強される状態を考えてみよう。
先ほどの母音の「い」の山型のスペクトルをノイズ音源と考え、ガウス分布を当てはめてみる。下図の様に、赤い破線がガウス分布の曲線、数字は鋭いピークの強さになる。

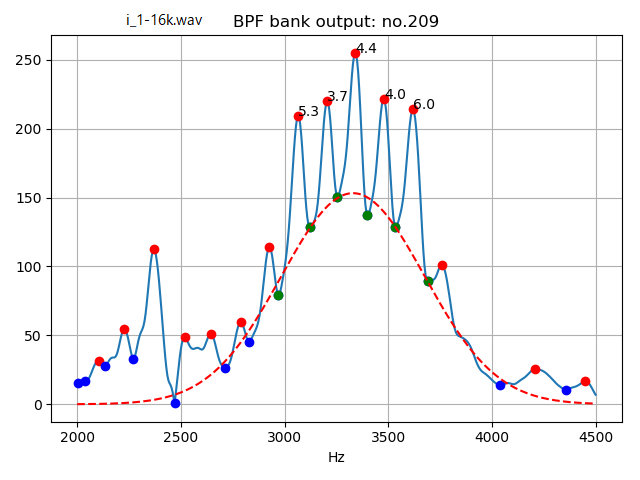
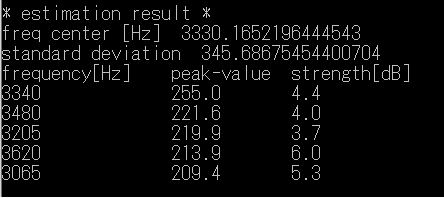
ノイズ源をガウス分布として近似したときの、中心周波数と偏差、そして、増強された鋭いピーク周波数の場所で、推定された音源のガウス分布から、何ｄＢ大きいかによって共鳴の強さを評価すると以下のようになる。

同様に、摩擦音の「し」のはじめの子音の部分に適用した場合は、以下の様になる。

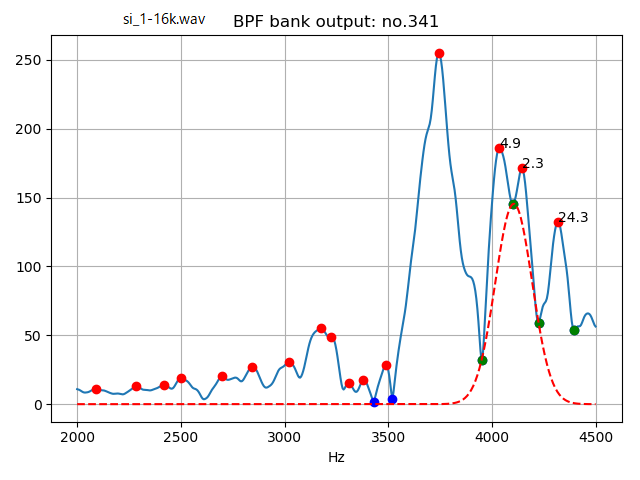
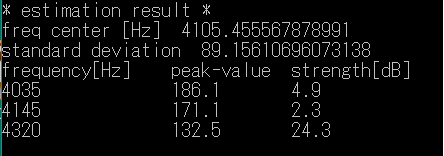
２管声道モデルの近似

下図の下段の絵は、母音の「い」の音声の、２ＫＨｚ周波数を超える周波数特性のピークとドロップピーク（上段の赤と青のマークの箇所）が２管声道モデルと一致するようにして求めた、声道の長さと断面積の推定である。

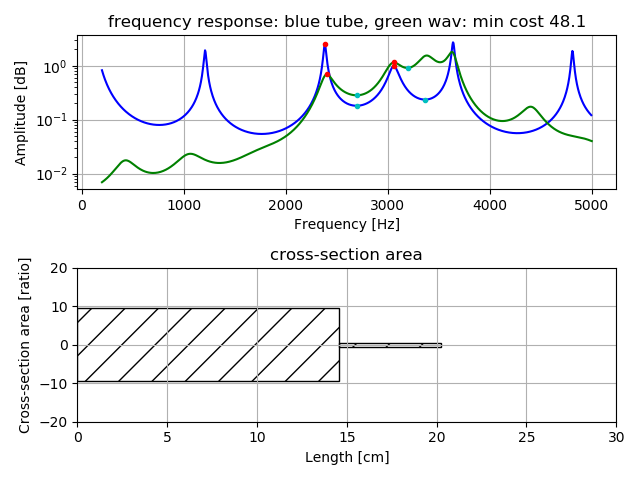
２管声道モデルの推定の説明は、2管モデル・3管モデルによる声道の推定のこころみ　を参考にして欲しい。

参考までに、上記で使ったpythonプログラムをおいておきます。使い方はzipファイルを解凍した中にあるREADME.txtを見てください。

No.1 2019年4月23日

Home page