最小位相のFIRフィルタ
─直線位相FIRフィルタから、ヒルベルトの関係とFFTを使って、近似的な最小位相FIRフィルタを求める─
直線位相のFIRフィルタから ヒルベルトの関係と 2のべき乗の長さのFFTを使って 長さは直線位相と同じの 近似的な最小位相のFIRフィルタのイ
ンパルス応答を求めてみた。 完璧な最小位相を得ようすると、零点を求めるための高次代数方程式を解く問題にぶつかる。(最小位相は零点がすべて単位円内
のあるため。零点を求める必要がる。) 次数が小さいならばよいが、200~300次の問題を解くのは難しいそうだ。そこで、厳密な最小位相ではないけれ
ども、実用的には使える、だいたい、最小位相の波形に近いフィルタができないかどうかを検討してみた。
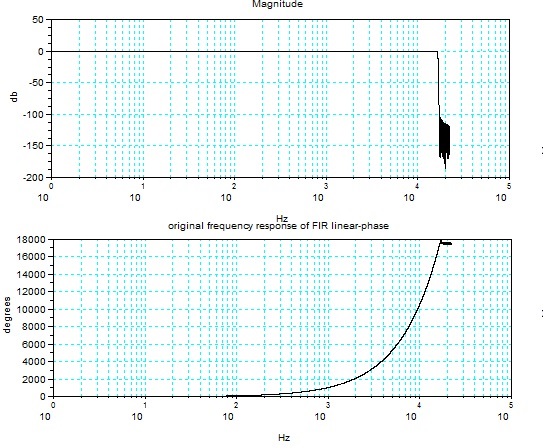
下記の図は、元になる直線位相FIRフィルタの特性である。ローパスフィルタである。サンプリング周波数44.1KHz、カットオフ周波数はサンプリング周波数の半分(ナイキスト周波数)の0.75倍(16.5375kHz=
44.1kHz*1/2*0.75)、減衰域では100dB以上の減衰が取れるように設計したものである。この直線位相FIRフィルタの長さは259個で
ある。(ほかによくあるので直線位相FIRフィルタの設計の説明は省略する。)
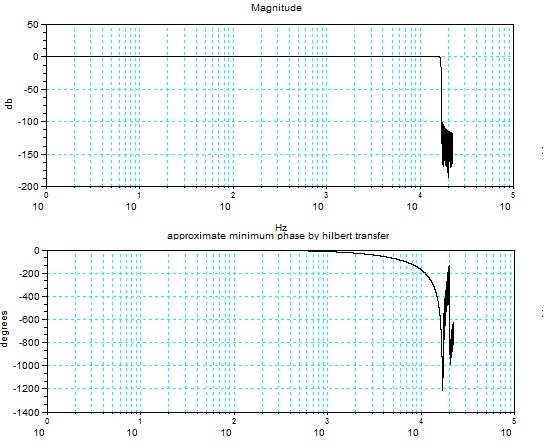
下図はヒルベルトの関係とFFTを使って、上図の周波数の振幅特性から最小位相(下段の位相特性)を求めたもの。離散的な変換を使っているので、ここでの値は最小位相の近似値となっている。
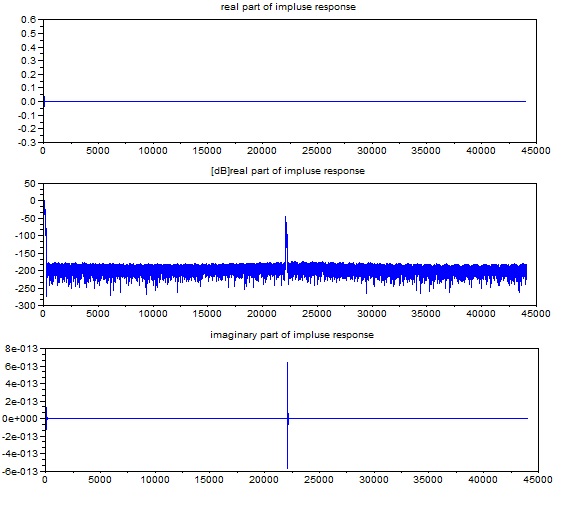
下図は、もとめた最小位相をもつ複素数の周波数特性をFFTで時間軸の値に変換してたもので、これをフィルタのインパルス応答として使う。FFTした結果
は、ほ
んらい複素数であるが、虚数部分は3段目の図のように(10のマイナス13乗のオーダーであり)かなり小さいので、以後、実数部だけ使ってフィルタを構成
することを考える。2段目の図は、普通の振幅表示だと値が小さすぎてわかりずらいので、実部の絶対値を一番頭
の値を基準にdB(10のLOGして20倍)表示したものである。最小位相なので、波形の大きな部分は(つまりエネルギーは)はじまりの方に集中している
ことがわかる。減衰をともなった繰り返し(中間地点で繰り返しピークをもつ)周期が見える。(周期性をもつらしい。)
下図は、インパルス応答の長さの違いによる周波数応答の比較で、サンプリング周波数と同じ個数の長さの場合と、もとの直線位相FIRフィルタのインパルス
応答と同じ場合の比較である。最小位相フィルタはインパルス応答のはじまりの方に(波形が)詰まっているはずなので、もともとの直線位相FIRフィルタと
同程度の長さでも周波数特性が再現できていることが期待される。
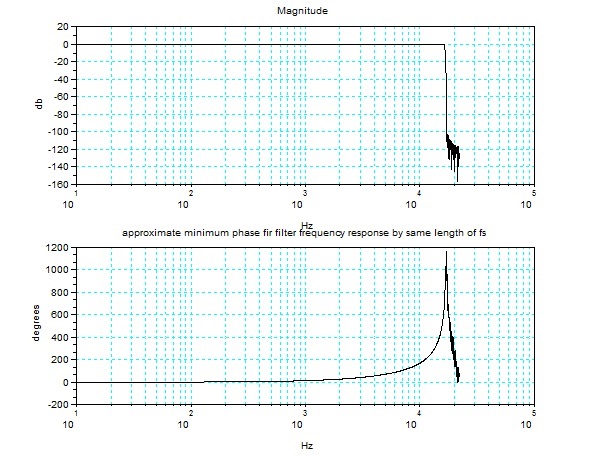
上図:サンプリング周波数と同じ個数の長さの場合
下図:もとの直線位相FIRフィルタのインパルス応答と同じ場合
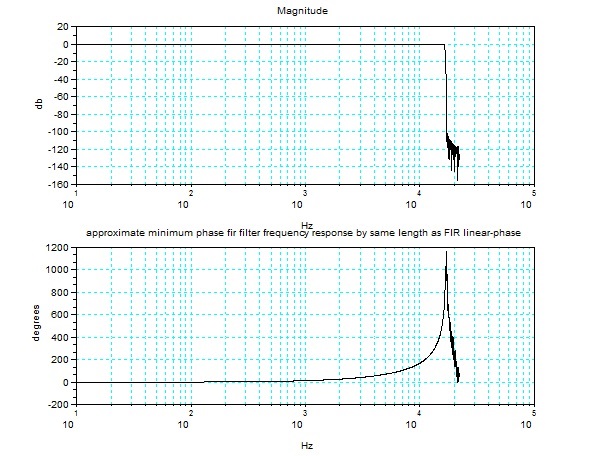
今までは、FFTの長さをサンプリング周波数と同じとして計算してきたが、FFTの長さの違いによって計算されたインパルス応答の波形がどうかわるのか1
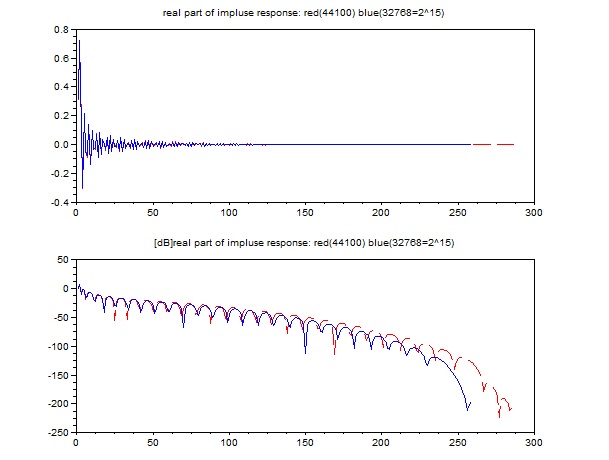
例を示す。下図は
FFTの長さが 赤色が44100、青色が32768(2のべき乗の値)で計算した結果で、直線位相FIRフィルタの長さと同じ長さの先頭のデータを比較
たものである。この例では、(赤色に青色が重なっていて)それほど大きな違いはないが、基本的にカットオフ周波数(の比)が同じならば同じ結果が得られそ
うだが、例えば長さがもっと短い1000の場合では違いは大きくなる。
最小位相の場合は、零点がすべて単位円内になるが、 今回の近似的な最小位相フィルタでは、258個の零点の中で単位円外にはみ出しているものが24個ある。完璧な最小位相にはなっていない。しかし、外側にあっても単位円からズレは小さいので 極端大きな位相の遅れはないだろうと思われる。
この直線位相FIRフィルタから近似的な最小位相FIRフィルタを求めるために使った
数値演算ライブラリ
SCILAB用のサンプルプログラムを参考までに以下に紹介します。 このサンプルプログラムの動作保証はありませんのであしからず。
//------------------------------------------------------------------------------
// a study of hilbert transfer by scilab-4.1.2
// to get FIR min-phase from FIR linear-phase
// ..............................................................................
// WARNING: This program may have some bugs and you may modify this program.
// Everything done by your own risk, if you use this program.
//------------------------------------------------------------------------------
//(1) read point data
disp('making data...');
fs=44100.0; // sampling frequency
gensui_A0=100; //dB
gensui_haba0=0.1/2; //
fc=0.75/2; // cut off frequency
//
alfa0= 0.1102 * (gensui_A0 - 8.7);
KS= int( (gensui_A0 - 8) / (2.285 * 2 * %pi * gensui_haba0) + 1);
K=KS;
nsize0=2*K+1;
disp(nsize0,'nsize0=');
// fir lpf coefficient
wc=2. * %pi * fc;
a=zeros(1, nsize0);
a(K+1)= wc / %pi;
for m=K-1:-1:0
a(m+1)= sin( (K-m) * wc) / ((K-m) * %pi);
a(2 * K - m + 1) = a(m+1);
end
// Kaiser window
win0=window('kr',length(a),alfa0);
a= a .* win0;
// Log & plot
xIc=zeros(nsize0,1);
for i=1:nsize0
xIc(nsize0 - i + 1)= a(i);
end
bunsi2=poly(xIc,'z','coeff');
xHi=syslin('d',bunsi2,1);
df0 = 1.0 / fs; ////df0= 2.0 * %pi / fs;
freqdx = 0: df0: ( 1 - df0); ////0: df0: ( 2 * %pi - df0);
[frq0, repf0]=repfreq(xHi,freqdx);
H_list=abs( repf0);
repf0_stock=repf0;
//----------------------------------
// (5) hilbert transfer by FFT
// H(z)=ln(|H(z)|) + j arg(H(z))
//
lnH_list=log(H_list); // ln(|H(input)|)
// More long n0, approximation of minimum phase will be good.
n0=length(lnH_list);
// h(n) is like hilbert filter
// h(n) is un(n) defined in Oppenheim & Schafer, Digital Signal Processing, page 19 (下)
h=zeros(lnH_list);
h(1)=1; // h(1)=1
if modulo(n0,2)==0 then
h(n0/2+1)=1;
h(2:n0/2)=2;
else
h(2:(n0+1)/2)=2;
end;
IFFT0=fft(lnH_list,1); //dft(lnH_list,1); the inverse transform normalized by 1/n
FFT0=fft(IFFT0 .* h,-1); // dft(IFFT0 .* h,-1); x(k)=sum over m from 1 to n of a(m)*exp(-2i*pi*(m-1)*(k-1)/n)
// imag(FFT0) is approximate minimum phase
ComplexH_list=zeros(H_list);
for i=1:n0
ComplexH_list(i)= H_list(i) * exp( %i * imag(FFT0(i)));
end
//----------------------------------
// (6) require impluse response by FFT
//--------------------------------------------------
IRESP0=fft(ComplexH_list,1); // complex impluse response // dft(ComplexH_list,1);
IRESP0R=real(IRESP0); // get real part only
//--------------------------------------------------------
// (0) misc function for display
start_freq=10.0;
end_freq=(fs/2.0) - 10.0;
step_freq=2000.0; // many is good
scale_mode=1; // 0 linear, 1 log
function [freqa, freqd, kosuu]=get_freqs()
//
mode0=scale_mode;
if end_freq > (1.1 * (fs/2.0)) then
end_freq= 0.9 * (fs/2.0);
end
if mode0==0 then // linear scale
step_freq=(end_freq-start_freq)/step_freq;
freqa=(start_freq:step_freq:end_freq);
freqd=((start_freq/fs):(step_freq/fs):(end_freq/fs));
end
if mode0==1 then // log scale
step0= (log(end_freq) - log(start_freq)) / step_freq;
bairitu0= exp( step0 );
freqa=zeros(1,2);
freqd=zeros(1,2);
freqa(1)=start_freq;
freqd(1)=freqa(1)/fs;
for v=1:int(step_freq)
freqa(v+1)=freqa(v) * bairitu0;
freqd(v+1)=freqa(v)/fs;
end
end
s0=size(freqa);
kosuu=s0(1,2);
endfunction
//--------------------------------------------------------
//(7) Output display
wb0=xget('window'); // stack old window
xset('window',0); // create new windows
clf();
[db0,phi0]=dbphi(repf0_stock);
//gainplot(freqa,db0,phi0);
bode(fs * freqdx(1,2:fs/2), db0(1,2:fs/2),phi0(1,2:fs/2));
xtitle('original frequency response of FIR linear-phase');
xset('window',1); // create new windows
clf();
[db0,phi0]=dbphi(ComplexH_list);
//gainplot(freqa,db0,phi0);
bode(fs * freqdx(1,2:fs/2), db0(1,2:fs/2),phi0(1,2:fs/2));
xtitle('approximate minimum phase by hilbert transfer');
xset('window',2); // create new windows
clf();
subplot(311);
plot(real(IRESP0));
xtitle('real part of impluse response');
subplot(312);
plot(20.0 * log10( abs(real(IRESP0) / real(IRESP0(1)))));
xtitle('[dB]real part of impluse response');
subplot(313);
plot(imag(IRESP0));
xtitle('imaginary part of impluse response');
//------------------------------------------
// How long need of impluse response length enough ?
SampleL=length(a); //as same as FIR linear-phase
xIc=zeros(SampleL,1);
for i=1:SampleL
xIc(i)= real(IRESP0(i));
end
bunsi2=poly(xIc,'z','coeff');
xHi=syslin('d',bunsi2,1);
xset('window',3); // create new windows
clf();
[freqa, freqd, kosuu]=get_freqs();
[frq0, repf0]=repfreq(xHi,freqd);
[db0,phi0]=dbphi(repf0);;
bode(freqa, db0, phi0);
xtitle('approximate minimum phase fir filter frequency response by same length as FIR linear-phase');
// Get roots
xIc2=xIc / xIc(1); // moniic At fast coeff become 1
xIc2= xIc2(length(xIc2):-1:1); // Gyakuten suru
p1=poly(xIc2,"x","coeff");
k1=roots(p1);
disp("roots are");
k1
v1=poly(k1,"x"); // get coefficient from roots, but, it's wrong !
// check over unit circle
disp("abs(roots) >= 1.0");
for i=1:length(k1)
if abs(k1(i)) >= 1 then
disp( (abs(k1(i)) - 1.0), abs(k1(i)), k1(i));
end
end
// data save
//disp('write data...');
//writb('writeout',xIc); // binary write head(4) + data 8 byte + last(4)
//----------------------------------------------
xset('window',wb0);
SampleL=fs; // length is as same as fs
xIc=zeros(SampleL,1);
for i=1:SampleL
xIc(i)= real(IRESP0(i));
end
bunsi2=poly(xIc,'z','coeff');
xHi=syslin('d',bunsi2,1);
xset('window',4); // create new windows
clf();
[freqa, freqd, kosuu]=get_freqs();
[frq0, repf0]=repfreq(xHi,freqd);
[db0,phi0]=dbphi(repf0);
bode(freqa, db0,phi0);
xtitle('approximate minimum phase fir filter frequency response by same length of fs');
xset('window',wb0);
零点の値とフィルタの係数
零点を求めるため、scilab の
roots関数を使っている。この零点から逆にフィルタの係数を計算しようとすると、途中、まったくデタラメな数値となってしまい使えない。理由は、計算
の精度にあるようだ。Windows 32bit scilabの場合、多分、long double (80bit?)
で計算しているようで 10進数の桁数だと、二十数桁程度と思われる(外観上は double(64bit))。 例えば、10進数で70桁の多倍長で計
算すると、だいたい、もとのフィルタの係数に戻るようだ。
scilabで計算した、単位円外にある零点の値とその大きさ(絶対値)は
- 0.9981685 + 0.0606763i 1.0000109
- 0.9981685 - 0.0606763i 1.0000109
- 0.9940501 + 0.1090456i 1.0000133
- 0.9940501 - 0.1090456i 1.0000133
- 0.9911001 + 0.1331263i 1.000001
- 0.9911001 - 0.1331263i 1.000001
- 0.9678601 + 0.2518859i 1.0000998
- 0.9678601 - 0.2518859i 1.0000998
- 0.9305723 + 0.3662988i 1.0000698
- 0.9305723 - 0.3662988i 1.0000698
- 0.9214989 + 0.3884572i 1.0000296
- 0.9214989 - 0.3884572i 1.0000296
- 0.8914444 + 0.4531880i 1.0000263
- 0.8914444 - 0.4531880i 1.0000263
- 0.8453362 + 0.5342520i 1.0000092
- 0.8453362 - 0.5342520i 1.0000092
- 0.8330395 + 0.5533066i 1.0000515
- 0.8330395 - 0.5533066i 1.0000515
- 0.8205471 + 0.5716898i 1.0000634
- 0.8205471 - 0.5716898i 1.0000634
- 0.7957266 + 0.6057725i 1.0000706
- 0.7957266 - 0.6057725i 1.0000706
- 0.7654254 + 0.6435521i 1.0000177
- 0.7654254 - 0.6435521i 1.0000177
と、この例では 単位円の大きさ1からの はみ出し量は小さい。
また、零点、根を求めるのあたり(多倍長で計算すると計算時間が多くなるのである程度収束してから) 途中から 多倍長で計算しても、単位円外の個数の数は変わらないようである。
No.2 2015年8月16日





