非線形の最小二乗法の解法の、
数値演算ライブラリ
SCILABのleastsq を使って、
音声の波形の一部を
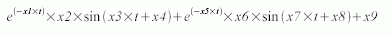
の形式の、指数関数EXP * SIN波の合成波で 近似してみよう。
42ポイントの音声の波形データ ym が
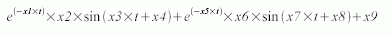
の式で計算される値に合うように、
x1 から x9 までの9個の係数 x0 を求めるサンプルのtest3.sciを以下に示す。
m= 42;
tm=[ 0.000000E+00,
1.000000E+00,
2.000000E+00,
3.000000E+00,
4.000000E+00,
5.000000E+00,
6.000000E+00,
7.000000E+00,
8.000000E+00,
9.000000E+00,
1.000000E+01,
1.100000E+01,
1.200000E+01,
1.300000E+01,
1.400000E+01,
1.500000E+01,
1.600000E+01,
1.700000E+01,
1.800000E+01,
1.900000E+01,
2.000000E+01,
2.100000E+01,
2.200000E+01,
2.300000E+01,
2.400000E+01,
2.500000E+01,
2.600000E+01,
2.700000E+01,
2.800000E+01,
2.900000E+01,
3.000000E+01,
3.100000E+01,
3.200000E+01,
3.300000E+01,
3.400000E+01,
3.500000E+01,
3.600000E+01,
3.700000E+01,
3.800000E+01,
3.900000E+01,
4.000000E+01,
4.100000E+01];
ym=[ 1.280000E+03,
4.864000E+03,
8.448000E+03,
1.152000E+04,
1.433600E+04,
1.664000E+04,
1.817600E+04,
1.945600E+04,
2.022400E+04,
2.022400E+04,
1.971200E+04,
1.868800E+04,
1.715200E+04,
1.484800E+04,
1.228800E+04,
9.216000E+03,
5.632000E+03,
2.048000E+03,
-1.536000E+03,
-5.120000E+03,
-8.192000E+03,
-1.075200E+04,
-1.280000E+04,
-1.408000E+04,
-1.510400E+04,
-1.510400E+04,
-1.484800E+04,
-1.408000E+04,
-1.280000E+04,
-1.126400E+04,
-9.472000E+03,
-7.936000E+03,
-6.656000E+03,
-5.632000E+03,
-5.120000E+03,
-4.864000E+03,
-5.120000E+03,
-5.632000E+03,
-6.400000E+03,
-7.168000E+03,
-7.936000E+03,
-8.448000E+03];
wm=ones(m,1);
// estimated function
// initial parameter
x0 = [ 1.190476E-02 ; 2.022400E+04 ; 1.495997E-01
; 0.000000E+00 ; 1.190476E-02 ; 1.011200E+04 ;
1.795196E-01 ; 5.235988E-01 ; 4.754286E+02];
function y = yth(t, x)
y = exp(-x(1)*t). * ( x(2) * sin(x(3)*t + x(4))) +
exp(-x(5)*t). * (x(6) * sin(x(7)*t + x(8)) ) + x(9)
endfunction
function e = myfun(x, tm, ym, wm)
e = wm.*( yth(tm, x) - ym )
endfunction
// 1- the simplest call
[f,xopt, gropt] = leastsq(list(myfun,tm,ym,wm),x0)
//... call plot
plot(tm,ym,'+',tm,yth(tm,xopt),'-')
// File Out
//write( "c:\test3XOPT.dat" , xopt)
//write( "c:\test4GROPT.dat" , gropt)
//---------------------------------------------------------------
// A solution:
// x0=[ -0.039601; 20201.361158; 0.182714; -0.529008; -0.055432;
10046.790109; 0.209052; 1.731614; 2263.041282];
//
// Translated description:
// exp(873.196 * t ) * ( 20201 * sin( 641 * t -30)) + exp(1222.283 * t
) * ( 10047 * sin( 734 * t + 99)) + 2263
//
//
//---------------------------------------------------------------
このサンプルを実際に動作させるためには、おそらく、
ご使用されるプログラミング環境に合わせて修正・変更・追加などが必要です。
万一、このサンプルを動作させる場合は、あなたの責任においておこなってください。
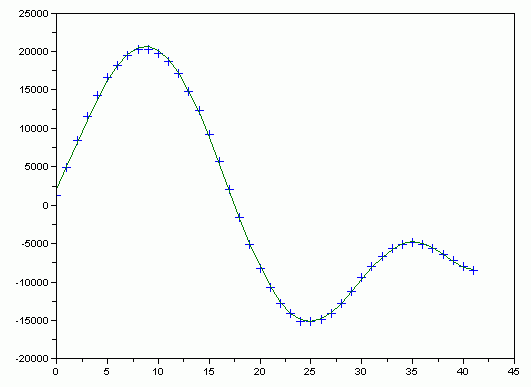
上記のtest3.sci をscilabに読みこませて実行すると、
下図の様な結果が得られる。図の中の+マークが元の音声の波形の一部の42ポイントのデータで、
実線は求められた係数 x0 を使って
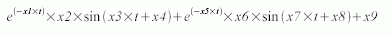
をプロットしたものである。
初期値である test3.sciの中の
// initial parameter の以下の x0 =[ ]の中の値は、
ある程度 当たるように あらかじめ(人が考えて)設定しておかないと、計算が上手くいかないので注意が必要だ。
No.2 2007年7月1日