音声認識について考える　－内部構造によるパターン認識の研究

音声認識について考える

- 音声の内部構造によるパターン認識の研究 -

作者 Shun

English Japanese

<音声認識について考える>

<メッセージ>
　音声科学の研究は、日常生活に役立つ成果をもたらしています。これからさらに発展するためには、まだ明確でない音声認識の原理の解明が不可欠のように感じています。現在広く行われている表面的な特徴量を比較するパターン認識ではなく、同じ意味のパターンの形が多様に変化する、パターンの多様性を説明できる音声認識技術が必要と思われます。

音声認識の原理がさらに解明されて行き音声科学が発展することを望みながら、このホームページを作成しました。

<音声のパターン認識についての簡単な説明>

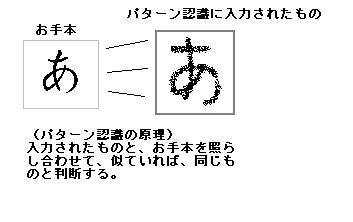
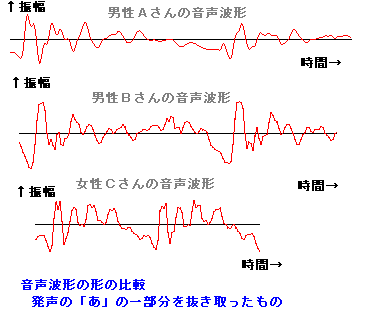
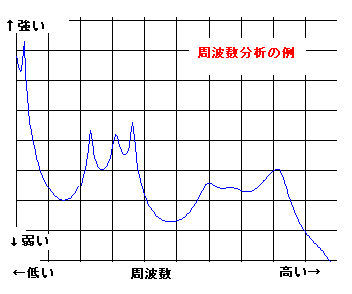
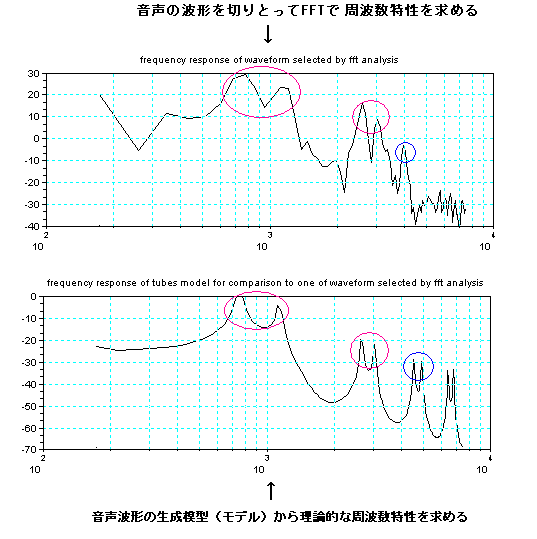
もっとも簡単なパターン認識の方法は、お手本と見比べて同じものなら、それと判断するものである。例えば、日本語の片かなの「あ」を認識することを考えてみよう。右の図を見て欲しい。パターン認識する機械に、入力されたもの（右の手書きの「あ」）を、お手本（左の楷書の「あ」）とところどころ見比べてみて、だいたい同じものならば、入力されたものを「あ」と判断する。このパターン認識の方法は、入力されるものが、お手本とそれほど違わないときには上手く働くのだが、現実の世の中はそう甘くはない。

さて、人が発声する声をマイクを使ってAD変換してコンピューターに取りんだ波形（縦軸が入力電圧の振幅、横が時間ｍS）
の例を見てみよう。右図は３人分の「あ」の発声の波形の一部分を示す。３つの波形を比べれ見ると分かるとうり、同じ「あ」の発声であっても、波形の形は似ているようであり、また、違いありそうなことが分かる。つまり、実際の音声の波形は人や話し方で違いがあるのである。 もし、お手本を１個だけもっていたとしても、音声は人や話し方によって違いがあるので、認識が上手くいきそうにないことが推測できる。音声認識のソフトで事前に学習するのは、その人や環境（マイクやアンプの周波数特性や話し方　例えば緊張しているとか）に合うようにお手本をチューニングする作業をしているのだ。
　
通常、音声の波形そのものをパターン認識に使うことは少なく、より適した尺度に変換したものを使うことが多い。例えば、音声波形を周波数分析すると、右図のように、幾つかの周波数で強さのピーク（ホルマントと呼ばれる）があらわれることが知られている。
ピークの逆の現象（抑圧される部分）も知られている。古くから、これらの特徴が音に「い」とか「あ」とかなどの意味付けしていると言われている。
　
さらに、時間の経過の順に周波数分析の結果を並べていくと、音声信号のなかのピークの周波数や強さなどは時間的になだらかに変動していることがわかる。逆に、人工的に変動しない音声をつくってみるとよく聞き取れない。

人がどのように音声から「あ」とか「い」とか「か」などを識別判断しているのかについては、長い間　数々の研究が行われているが、１００％明確に説明できる認識理論は　まだ　ないと言うのがホントのところであろう。

音声の波形の生成を理解してみよう

日本語5母音の特徴

音の構造の記述，変化モデル（子音）

音声の内部構造によるパターン認識とは

音声信号の分布と構造の極点の関係について

音声技術の人間社会（Mankind Social）への貢献

音声研究のリンク集

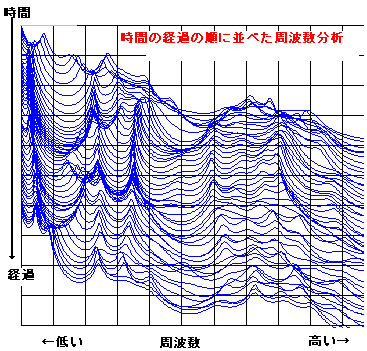（注）上図の２つは、スペクトルの変化度合いを見やすくするため、音声のLPC分析による周波数分析の結果を描いている。

No.16 作成　2015年9月24日
変更　2018年11月20日

「研究とは、数々の思考錯誤を経て到達するものである。」
"Machine works within pre-programed procedure. Do you expect human nature for that tool?"

　音声認識のパターン認識の方法は周波数特性であるスペクトルまたはその逆変換であるケプストラムを単位としてパターンを比較することが多く行われているが、パターンを比較する単位としてはもっと細かく見ないと十分に違いが見えてこないように思える。そこで、より詳しく、音声の周波帯域ごとの成分と波形の時間変化について観察してみよう。

<音声の波形を分析する>

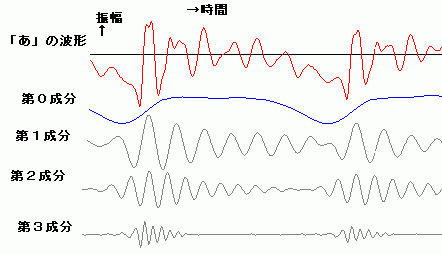
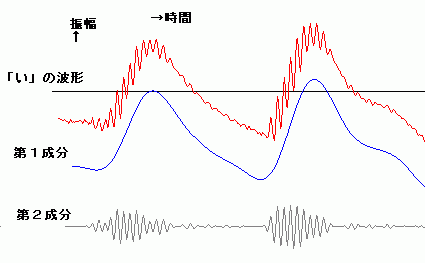
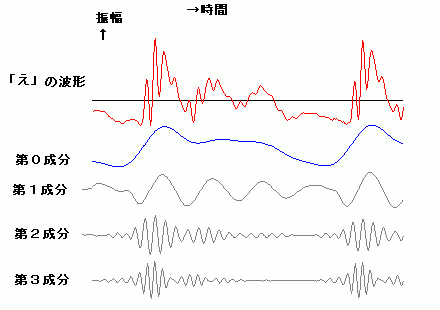
　音声の波形は幾つかの構成成分に分解できるようだ。右の図は、人が「あ」と発声したものをコンピューターに取りこんで、てきとうな周波数帯域ごとの成分を計算して、構成成分を求めたものである。赤色のぎざぎざした波形が、もとの「あ」の波形である。その下の、第０成分から第３成分までの4つの波形が示してあるが、この４つの波形を全部足し合わせて合成すると、おおよそ、赤色のもとの「あ」の波形の形になる。青色の波形は主に発声時の喉の振動から起因する成分で、音程の高さを決める。下の灰色の波形は、喉の振動がトリガーとなって発生するより高い振動数をもつ信号たちで、喉の信号が起点する周期で、バースト状に発生する。さらによく観察すると、それは、単純な正弦波ではない。

「あ」は、より高い振動数をもつ何段かの階層的な成分により構成されていたが、次に、「い」を見てみよう。「い」の場合は、主に、土台となる成分（右図では青色の第1成分）と、それにまとわりつく雑音の様なごちゃごちゃした信号（右図では灰色の第２成分）から、構成される。仮に、「い」から第２成分を差し引くと、「う」に聞こえる。

次に、「え」の場合を見てみよう。「え」は、主に、それだけ聞くと「お」に聞こえる第１成分と、「え」を特徴付ける第２成分から構成されるようだ。第３成分を付加することで　より「え」ぽっく聞こえるようになる。

　以上に示したものは安定した波形の一部分を抜き出したものである。実際の発声時には、動的な生成が行われて安定した波形になっていく。波形の安定した部分よりむしろ、動的に生成が行われる部分の方で、人は音節の判別していると思われる。このことが、連続発声したものから一部分を抜き取って聞くと（連続音で聞こえた音節と違った）別の音節の音に聞こえる現象を説明する手がかりになると予想している。

動的な変動を観察するために、ちょっと分かりにくいが、単音節の発声の初期の過渡的な部分の波形の例（「あ」、「い」、「う」、「え」、「お」）をリンクしておこう。

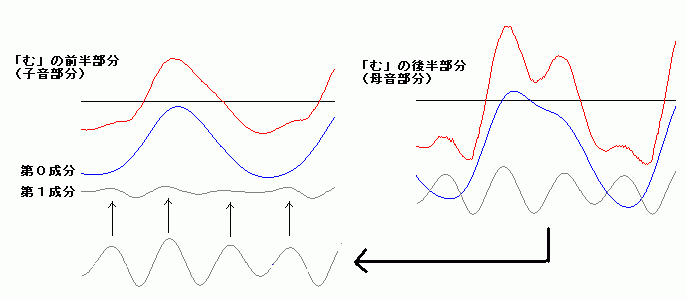
　さて、「あ」は元気がいい波形たちを誘起させるが、逆に音を抑圧する物もある。下図は、ま行の「む(mu)」の前半の子音部分と後半の母音部分を比較したものである。子音部分と母音部分は、同じ周期性をもった成分（灰色）をもっている。しかし、子音部分では母音部分に比べて振幅の大きさが極端に小さく、抑え込まれていることが分かる。母音部分になって、抑えこみから解放されて、青色の波形ともども元気がある波形なる。
参考に、単音節の「ま(ma)」を発声したときのmからaへの変化の波形をリンクしておこう。

　一般的に、子音部分はまったく同じと言う訳ではなく、後続する母音に引きずられて（後続する母音の特徴を内にもつように）変形する傾向があるようだ。

No.7 作成　2007年5月13日

<音声の構成成分の記述>

学校の化学の授業で、例えば、水は H2O、二酸化炭素は CO2　の様に元素記号をつかってその構成を表現できることを学んだと思う。ここでは、音声の音についても、音の各成分によって構成を表現することを試みてみよう。

もうひとつ、化学と違うところは、化学では、例えば、酸素元素のOはどこでも共通利用可能なものであるのに対して、音声の場合は、成分の測定値は変化し、各成分は互いの相対的な関係で決定されるということだ。　つまり、人間の発話器官はまちまちで全員が絶対的なまったく同じものを発声することはできないけれども共通に理解できるという要求のため、相対的な量（例えば周波数の比など）とその基点となるもの（キー）を使って　評価されるものになっていると考えられる。

また、もう一つ重要なことは、各成分は単独独立的な存在ではなく、共通の発生源（音源）から発生しているので、関係していると言うことだ。（例えば、声門の変化の３つのパターンが成分の波形に現れている。）　音声信号は”各成分の和”で成る。共通の発生源で関係しているのに、ある成分だけ勝手に変更してしまうと、壊れて音の品質が悪くなるかもしれない。
例えば、構成要素の例としてフォルマンを考えてみよう。もし、第１フォルマントと第２フォルマントが分かれば、その構造によって生み出される３番目のフォルマントの存在場所を予測できるはずである。このようにして、構造を当てはめていくとこができるだろう。

No.11 作成　2014年3月11日
No.12　追記　2014年5月30日
No.13c 追記　2014年12月17日

< 日本語5母音の特徴 >

　母音は声道の共鳴周波数のホルマントによって特徴付けされていると言うのが通説であるが、ここでは、ちょっと違う見かたをしてみよう。

　日本語の５つの母音のなかで、「あ」と「う」の２つは基本的な存在である。

「あ」の特徴は、２つの波を使って口からの音の放射効率が最大になるように、放射する波が近接してできるだけ揃うになっているのが特徴である（参考）。この波の高調波も、揃って高い周波数領域に現れる。スピーカーで例えるならばホーンスピーカーの効果に類似したものである。
逆に、「え」は、舌によって放射する波をわざと調整して、低い方はペアがなく、高い周波数領域の方だけ、波が近接して揃うようにしている（参考）。

「お」の音は、「あ」の音を起点として、それに「う」の効果をつなぎ合わせたものである（仮説）（参考）。

「う」は色の無い音である。（口の中で）響いたことを示す、（３つ以上の）複数の波（高調波）がたっている。キーとなる近接した揃った波のペアが見当たらないか、あったとしても大きな唸りがない。どちらかと言うと特徴がないのが特徴なので、「う」はいろいろな形が存在する（参考）。

「い」は、「う」に更にノイズっぽい高域の成分を重畳した構造である（参考）。このノイズっぽい高域成分は口先の空間が狭くなって風が流れることによって生じるものであり、口先を狭めての発声であることを伝える。

日本語の母音の特徴として、以上のように推理している。

No.15 作成　2018年11月7日

<音の構造の記述，変化モデル>

日本語のサブセットとして９音からなる音の構造の記述方法を考えてみよう。

　　（日本語９音サブセットの内容）

「あ」、「は」、「さ」、「か」、「た」、「ま」、「な」、「ら」、「ぱ」　の９音から構成される。
残りの　「や」は　「い→あ」、　「わ」は　「う→あ」と変化するものとみなす。

「あ」　　前述の日本語5母音の特徴の項を参考して欲しい。
「は」　　有声波の替わりに、のどで発生するノイズを音源として、口の共鳴管システムに入力する。音は無声音であるがその共鳴管の特徴を有することになる。
「さ」　　口先の狭い隙間で、他にくらべて　周波数が高いところで分布するノイズを発生させる。
「か」　　強い息の吹きかけにより（ノイズ）、非線形現象の不定期に発生するバースト波を発生させて、口内で多少　共鳴させる。
「た」　　弱い息の吹きかけて（ノイズ）、すばやく音を立ち上げる。「た」には多くの形がある。
「ら」　　口蓋から舌を離す音からはじまる。（変化点の一例）　そして、各構成要素が段々と形つくられ最後に「あ」の形になる。　（「ら」のスペクトルの変化の一例）「な」の先頭はじめの部分を無くすと「ら」に聞こえる。
「ん」　　本来あるべきピークを鼻の効果で消音してしまい、かつ、高域周波数成分の音は無くす。
「ま」　　本来あるべきピークを消音するのと、高域周波数成分は主に２つのピークのみに消音する、２つの鼻に効果からはじめ、じょじょに鼻の効果を緩和させて　本来あるピークを復帰させる。
「な」　　「ま」と似ている。「ま」のときは最初から「あ」にあわせた口の形に対して、「な」は口先をつぼみかげんの状態から段々と最後の「あ」の形にしてゆく。
「ぱ」　　強い息とその反響からはじまる。

　上記の仮説にもとづいて作成したサンプル音と簡略な説明をこちらにのせておきます。

　母音においては口内を管（チューブ）とみなした静的なモデルを用いたが、これらの９音を記述するためには、更に　口先やどので発生するノイズと息　や　口と鼻の効果によるディップなど　の物理的な構造の可動限界に相当する、極（または停留点）または境界　の間の変化を記述できる必要があるであろう（仮説）。

No.15 作成　2009年5月23日

<音声波形の生成模型（モデル）の音声認識への利用>

　下の図は、ヒトが話した「あ」の波形の一部分の周波数特性と、音声波形の生成模型（モデル）による周波数特性との比較である。ヒトが話した「あ」に、特徴が似るように（下図の紫色の丸で囲ったところ）、生成模型（モデル）のパラメータを調整してみた。下の図を見るとわかるとうり、生成模型（モデル）でつくった特徴が、実際の音声にも含まれていることがわかる。（続き）

No.1 作成　2007年12月23日

< 音声の内部構造によるパターン認識とは>

　観測される表面的な特徴値の裏には、その生成過程である内部構造が隠されていると考える。例えば、観測された表面的な特徴量を耳に聞こえた音の波の姿とした場合、人間の喉の音源からその聞こえたその音の波が生成される過程を内部構造としてみよう。

「音声を生成する器官の作りや可動範囲の制約下で、
　その発生音が分離して認識できる条件を満たすため、
　意味ある音を生成する器官の配置は突き当りや停留点などにならざるおえない。
　そのため音素に対応するその配置構造は幾つかの種類に限定される。」

「構造で結びついて互いに制約されているため、音声を特徴つける各パラメーター（例：フォルマントの周波数の組など）はそれぞれ自由な独立した値は取れない。」

との予想のもと、

試験信号の中に、どの配置構造によるもの（その特定な構造から生成されるもの）が含まれるかを調べることでパターン認識するものである。

内部構造の推定とそれに基づくパターン認識の方法は、まだ、完成されたものではなく、仮説の段階にある。話す人や体調や周囲の環境によって音声の波形は色々である。絶対的なリファレンスになる値がある訳ではない。音の構成成分は互いの相対的な位置関係できまってくるので、解法は、その（内部）構造に上手くあてはめる問題（最適化）に帰着されるであろう。
「個々の種類からある自由度を持って音が生成されることにより、表面的な特徴量が持つ多様性が生じる。」とパターンのもつ多様性を説明しようとするものである。

内部構造と　パターン認識の手法化へ

また、音声だけではなく、例えば、ピアノの音の内部構造、バイオリンの音の内部構造など、人が認識できる音のそれぞれに内部構造をもつと考えられる。色々な音が混ざった音の中から、該当する内部構造をもつ音を検出することによって、聞き分けができるのかもしれない。

たとえば、ヒトの口の構造から発声できる音の種類を考えてみよう。
下の表は、人の声の音を認識するための案と仮説をしめしたものである。音から、要因を推定し、それらを組み合わせて、何の音かを判別する。

	推定するもの estimated factors	種類 kind	この特徴が存在する理由。または、決定つけるもの。 Reason why the feature exists. Or, principle to decide it
共鳴パラメーター resonance parameters	r1,l1	/a/	口からの放射効率最大の原理 principle of maximum radiation from mouth by using two waves
		/e/	１つと２つの波のよる停留値 stationary point by using one wave and two waves
		/u/,/i/	その他 other
	r1,l1,r2,l2	/o/	拡張方法　２管模型から３管模型へ。第1管と2管は口からの放射効率最大の原理、第2管と3管は「う」のようにつなぐ。 Extend method, from 2 tubes model to 3 tubes model. 1st and 2nd tube follows principle of maximum radiation, 2nd and 3rd follows like /u/.
	rl	口内での共鳴の効果の強さ rate of resonance effect in mouth
ノイズ noise	性質　 nature	定常,バースト constant,burst	流体の境界条件 turbulent boundary
	周波数分布 frequency range	/i/,/s/,/t/と /r/の開始時(start mark of /r/)	人の器官の物理的なつくりによる制約？ Are they determine by physical of human vocal organs ?
	重畳 superpose	単独、元を更に歪ませて発生（濁音） sonant( more disturb origin),independent	ノイズを付加する方法の種別 classification of noise superpose method
効果時間 effective duration	生存時間 survival rate	/t/,/p/	最小判定単位は１ピッチ程度？ Is the unit to judge a pitch duration ?
効果時間 effective duration	突発性 break	/p/	同上 same as above ?
消音された suppressed	消音された箇所 portion to be suppressed	/m/,/n/,/N(nn)/	後続の母音との比較 ? 鼻を使って音素数を増やしたい。 Compare with following vowel ? To increase kind by using nose effect
音程 tune	ピッチの変化 controlled pitch	平坦,上がり,下がり stable, rise, fall	状態変化はこの３つの組み合わせからなる。　音程を使って音素数を増やしたい。 any state will be composed from these 3 states. To increase kind by using tune.

また、ヒトがある場所から他の場所に移動するときに近道を選ぶように、音素の間の変化・変形のしかたは寄り道しないで行われるであろう。（参考）　　この寄り道しない原理と、口の物理的な可動範囲の制約から、音素が移り変わっていく構造の変化の仕方は、いくつかに、決められるであろう。確率的にみると、遷移確率が高いパス（または状態）が子音（または母音）に相当すると解釈し、（発声器官の）構造が同じため相対的な位置関係が不変にたもたれる変換によって、話者などの違いによる確率の分布の違いを吸収できるのではないだろうか。また、直前の状態からの行きやすさに依存するため、同じ子音記号の間でも、直前の状態におおじて、少し違ったものになるであろう。

効果音に相当する口の構造化だけではなく、その音源の構造化も考えなくてはならない。
つまり、識別は、効果としての口の構造と　その音源の構造を　推定することになる。

No.19 作成　2010年7月31日
No.20 追記 2013年6月23日
No.21 追記 2014年4月17日
No.22 追記 2014年5月5日
No.23 修正 2018年11月7日

「科学は常に不完全なものだ。」
"Science is semi- circle."

<　信号の中に含まれている構造をいかに抽出するか　>

観測された音信号の中に含まれる構造体を探ることを考える。　
普通、観測する音信号は構造体が予測する形に、ぴったり一致する形にはなっていない。そのため、全体の目標（構造からの予測値）から誤差小さくして合わせこむ方法では上手くいかない。
構造体が持つ特徴、通常、複数の要因が関係する特徴を把握しておいて、観測する信号の中に、その特徴を満たすものがあるかどうか、部分的に、ひとつづつ調べていくことになる。　一度に、いっぺんに、解析的に分析できるのが機械で処理するためには理想であるが、上手い方法が思いあたらない。

音声の認識ではないが、考え方を理解するための類似な例として、観測した信号の中から構造で束縛された２種類の信号を特定するための　ラフな全探索と最小2乗法を使った構造フィッティングの例と、
３個のフィルター（２個のピークを持つフィルターと１個のなだらかに減衰するフィルターの３個から構成される構造で表現する）で周波数特性を　順を追って合成する例をあげておこう。

No.2 作成 2015年2月14日

「彫刻家は、あらい木材の中に、姿を見る。」

<「う」と「お」の違いは響きにあり>

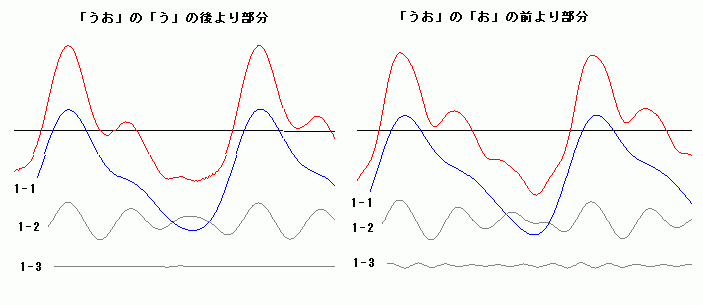
「う」と「お」の違いを探るため、「うお」と発声したときの波形成分を比較してみた。
下図は、「う」の後半と「お」の前半の部分を比較したものである。両者の違いは、１－３成分がはっきりと現れてきていることである。これは、発声している口の中での響き音（１－３）が追加されたことを意味すると考えられる。　

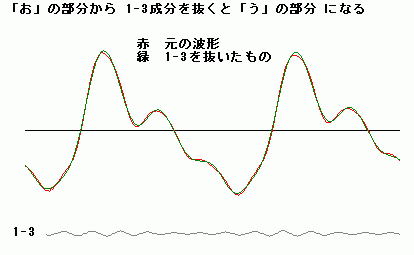ちなみに、「お」の前半の部分から１－３成分を抜きとった波形をつないで聞くと、「うお」は「う」のままのように聞こえる。上図は、赤色が「お」の前半部分と、緑色がそれから１－３成分を抜き取った波形を比較したものである。波形の形としてはほとんど同じように見えるが、聞くと違いがでるのである。
参考に、「う」から「お」にうつり変わるときの波形をリンクしておこう。

ちなみに、「おえ」と発声したときの「お」から「え」にうつり変わるときの波形もリンクしておこう。これを見ると、「お」から「え」の変化点で、第２成分が弱くなり、逆に第３成分（「え」の第２成分に相当）が強くなる、うつり変わりが見られる。この「おえ」の中から第２成分と第３成分の2つの成分だけを取り出して聞くとこのような音になる。

また、「うあ」（「うわ」）と発声したときの変化点、「う」から「あ」へのうつり変わり　つまり「わ」の波形もリンクしておこう。「う」から「あ」に変化する過程で第１成分の振動数が上昇して高くなっていることがわかる。しかし、振幅は大きくなっていくが第２成分の振動数の方は意外にも大きな変化はない。これは、「う」と「あ」で第２成分はほぼ同じ場所で響いているのであるが、「う」の方は高域カットフィルターのような狭い筒状の口なので、減衰してしまったと考えられる。

「う」と「あ」のもっとも大きな違いは、第１成分にある。「うあ」の第１成分のみを抜き出して聞いてみても、だいたい「うあ」と聞くことができる。下図は、「う」の区間のひとつと「あ」の区間のひとつを、波形とそのFFTスペクトル分析で比較したものである。さて、「う」の区間の波形を両側から押し縮めて、振動の周期がだいたい「あ」の区間の波形になるものを想像してみよう。どちらも、振動する波形であり、その概容に極端な差はない。しかし、この中に、「う」と「あ」を識別できる微細な違いが含まれていることになる。音素の認識には、従来の手法の分析レベルでは不足で、もっと微細なレベルも考慮しなくてはならないでのはないかと考えられる。
しかし、第１成分を更に細かく　構成成分を分析してみるとその違いがよく分かる。違いは、「うあ」の第１成分の第２成分、「うあ」の第1成分の第３成分に現れることがよく分かる。

FFTスペクトルの形は、窓の種類やFFT分析を計算する箇所によって、その形は変化するので一概には言えないが、例えば、上図の例では、左側の「う」にくらべて、右側の「あ」の方には、頂上の山（青色の↓）より周波数の低い側に微細な中腹の山（青色の↓）あることが見られる。ちなみに、周波数帯域のフィルターをかけて第１成分を計算して求めているので、全体のスペクトルの形が１つの山型になっている。

No.9 作成　2007年9月23日

< 子音の構造の例：　「か」音を「た」音に変換してみる>

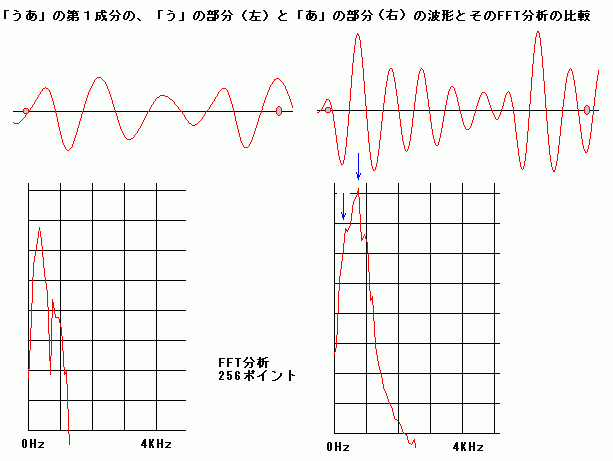
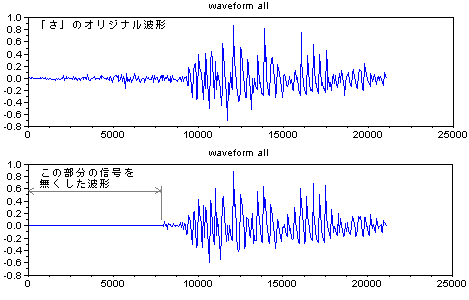
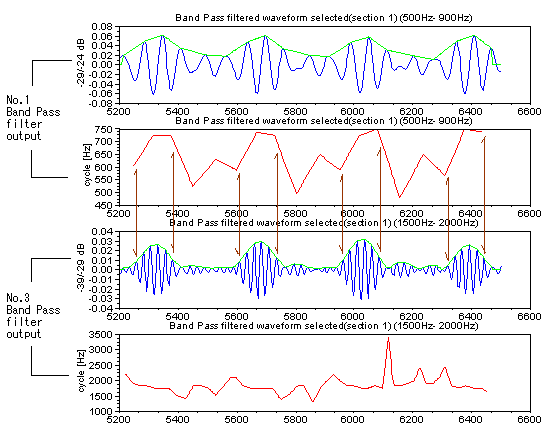
　構造的に見ると、「か」の音のはじめの部分は、発声するときに少し口が開いて口に空洞ができてそこで発生する音の成分と、息を吹いて発生する乱流による音の成分の、２重構造になっている。(資料)
それに対して、「た」の音のはじめは、口が閉じたところから行き成り息を吹きかけた成分のみが主な構成要素である。
右図の図の上の波形は、「か」の音の波形であるが、「か」の音のはじめの部分を低域カットフィルターをつかって成分を抜いてやると、右図の下の波形のようになり、「た」の音の様に聞こえるようになる。
乱流からの音はヒトの耳につきやすい音であるが、この種類の音の同定に周波数分析法では不足の感があるので、もっとよい分析法のアイデアが欲しいところである。ちなみに、空洞音や乱流の波形はヒトによってかなり異なる。
　
　無声音の部分、例えば、「か」「た」「さ」のはじめの部分に関しては、有声音に含まれる声門波のような基準となる同期信号が含まれていない。そこで、乱流によって突然発生するバースト波

　のありようを観察してみることにした。
複数のバンドパスフィルターで構成されるフィルターバンクをとうして、相対的に見比べて、それぞれの波形の特徴がないかどうかを少し長い時間長で観察してみることにした。右の６つの図は、どこに違いがあるかを見るために、「か」「た」「さ」の無声音部分について２人のヒトの波形を比較のために並べたものである。

また別の例では、「さ」の音のはじめの部分を無くして短くすると「た」の音のように聞こえるようになる（右図の一番下の波形）。このことから、「さ」の音は、口先に息を吹きかけて発生させている音が、ある時間の間　”安定して持続していること”　に意味があることが推測される。この部分が確率論的な認識をするためそれなりの時間間隔が要求されると、考えることができるかもしれない。
話題は変わるが、過去の研究から、濁音と非濁音の差は、声門からの信号との関係に時間差があることが知られている。

更に、は行の音（「は」「ひ」「ふ」「へ」「ほ」）のように、後続する母音の特徴を子音の部分に内在しているものもある。たとえば、「は」のはじめの部分と「ほ」のはじめの部分は違う　つくりになっているように。

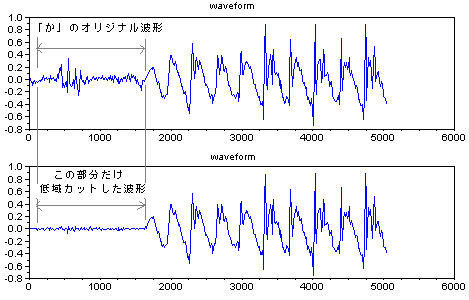　フィルターバンクから出力された波形を比較したもの　フィルターの分割数は８無声音部分の波形　　図をクリックすると拡大図になります

	Dさんの波形	Eさんの波形
「か」
「た」
「さ」

使用したフィルターバンクのプログラム

No.9 作成　2009年3月8日

< 「ん」の構造について　>

　日本語では、「ん」は単独で発声される。鼻に詰まった音に聞こえる一つの要因は、下図のNo.3 Band Pass filter outputのようにある区間だけ振幅が大きくなっている振幅変調（図中の緑の線）の中にあるかもしれない。この現象は、波形の周期が一定ではなく変動することによって、鼻の効果で吸収されたりされにくかったする部分ができることによって生じると考えられるかもしれない。つまり、鼻での効果で吸収される周波数は一定であるが、波形の方は変動していて　たまたま周期がうまくあうと吸収されて振幅レベルが下がる。No.3の振幅変調と比較すると、下図のNo.1 Band Pass filter outputの方は、声門の動きを反映したなだらかな山谷を繰り返す振幅変調（図中の緑の線）をしている。No.3で振幅が大きくなる区間は、No.1の波形で周波数が上昇している区間である（茶色の線で囲まれた区間）。つまり、No.3の方は、この周波数が上昇している区間に、反応して振幅が大きくなっているが、これ以外は、ある程度小さな振幅におさえこまれている。ちなみにNo.3の周波数変調を維持しながらNo.1と同様な振幅変調にしてしまうと鼻に詰まった感じが薄れてしまうようだ。また逆に、No.1 とNo.3の出力を足し合わせた音だけ聞いても、鼻に詰まった音のように聞きくことができる。
　「ん」の５バンドからなるフィルターバンクによる分析の一例を右図に示す。右図一番上に示すように、FFTによる周波数分析をしても、周波数特性は台形型となってしまい特徴があまりはっきりしない。

図をクリックすると拡大図になります

No.4 作成　2009年5月3日

<構成成分にもとづく音声のパターンマッチング>

　ヒトの音声は　ある決まった固定した周波数帯域に　主な構成成分があるわけではない。話すヒトや話し方によって、主な構成成分が形作られる周波数帯域は変動する。構成成分が周波数帯域のどこらへんにあるかを見積もるため、ある適当な音声区間でFFTによる周波数分析を行い、そのFFTの周波数特性の中で山になっている複数の部分の周波数帯域にそれぞれの構成成分があると初期値を仮定して探索を開始するようにした。構成にもとづくパターンマッチングは、決められた一通りの計算をすれば解を得ることができるような数学で解析的に問題を解くような手法はない。試み（method）で行ういろいろな形の信号の数値計算と　想定された形（構造）に当てはめる条件にあうものを探すために使う人工知能で考案された探索手法のようなものとの組み合わせになるであろう。しかし、実際には、うまく解に行き着けるかどうか、あまり見通しのよい方法ではない。音声の波形はヒトや時によっていろいろあるので探索中に条件に上手くマッチングした解に行き着く保障はない。そこで、種類の違う試み(method)を同時に並列に走らせるマルチスレッド型の探索をして　どこかのスレッドで上手くマッチングする解が見つかったら探索を停止するとした方がよいかもしれない。（マッチングと学習についての補足）
または、構造に関係したいろいろな特徴を特徴抽出値とする統計的なパターン認識の手法にのるかもしれない。

「特徴抽出の方法に王道はなし。」

　　探索の内容

基本的な周期の取り出し。　　　音の高さ、ピッチ、近接した波の干渉（ビート）などの分析の基礎となるものを取り出す。
声門波形と同期した成分たちの取り出し。　　成分の波形が声門波で変調がかかっていることを利用する。音源分離への応用もあるかも。　
調音ターゲット点へ向けての時間変化の軌跡の追跡。　　調音ターゲット点までの道はヒトによってそれぞれちょっと違うかもしれないが向かう点は同じ。　調音ターゲット点の構造の同定。

　時間的な変化は、合理的に行われると考えられる。周り道をする訳ではなく、口の物理的な可変性の中で両者の構造の間で近い道を通って変遷するものと思われる。(参考) 近いとは、共通につかえる部分はそのままで　まずは違いがあるところに注目して変遷させる。結果的に、それに伴って共通部分も影響を受けて変形することもありえるであろう。
　

　調音ターゲット点とは、ヒトが口舌を動かして調整しながら、目標である意図する音になった時点である。（補足説明）

近接する区間の関係で記述される例として、「は」の場合を右図に示す。区間１は子音部分の、区間２は母音部分の一部である。中段のfrequency response周波数特性の図を見ると、ともに、周波数特性上では、「あ」の特徴（紫色の丸で囲ったところ）をもつことが分かるが、下段のフィルターバンクからの出力を見ると、母音の区間２は声門波で同期がかかった信号群であるのに対して、子音の区間１の方の信号郡の秩序は弱い。「は」の場合、はじめの子音のところでは後続する母音の特徴をノイズぽい信号の中に内在させておいて、安定した特徴をもつ母音の音につないでいく構造になっている。

下図はフィルターバンクから出力された波形を比較したもの　
図をクリックすると拡大図になります

使用したフィルターバンクのプログラム

FFT分析スペクトルと２管模型からのスペクトルの比較によるパラメータの推定の例

　また、通常　構造は時間的に変遷するが、その例として、鼻音ではじまる「な」と「ま」の波形の例をここに示す。「な」の時間的な構成は、「鼻音」＋「ら」＋「あ」に対して、「ま」の方は「鼻音」＋「あ」の様になっている。

　普通の会話の中の音はその構造が崩れていることも多い。文字を書く形式にも、丁寧に書く楷書と文字を崩した行書や草書があるのに似ている。文章または単語としては自然に頭に入ってくるのであるが、その音声を細かく区切っていち音いち音ごとに聞いてみると、惰性で発声しているような不明瞭な音も含まれる。これを構造だけで認識するのは難しい。行書用と草書用の２種類のパターンをもつか、現代の音声認識の方法のように単語や文章の制約も絡めて全体で認識することが望ましいだろう。

No.14d 作成　2008年5月27日

「生成する能力と検出する能力は、表裏の関係にあるかもね。」

< 音声信号の分布と構造の極点の関係 >

　音声信号の分布は、音声を生成する構造上の極点(構造的にどついたところ。構造の種類に応じて複数個の極が存在する？）または停留点（中間点）に相当する箇所に分布の中心がある可能性があることが予想される（あっているかどうかは未確認）。また、峯松氏らの研究により　、分布群の構造不変の定理が知られている。仮に、話者よって音声信号の分布の仕方は違うが、音素（「あ」「い」「う」「え」「お」など）の相対的な位置関係は、ある変換を通して同じである解釈すると、　音素間の分布群の位置関係が　このホームページ扱っている構造に相当すると解釈できないであろうか。

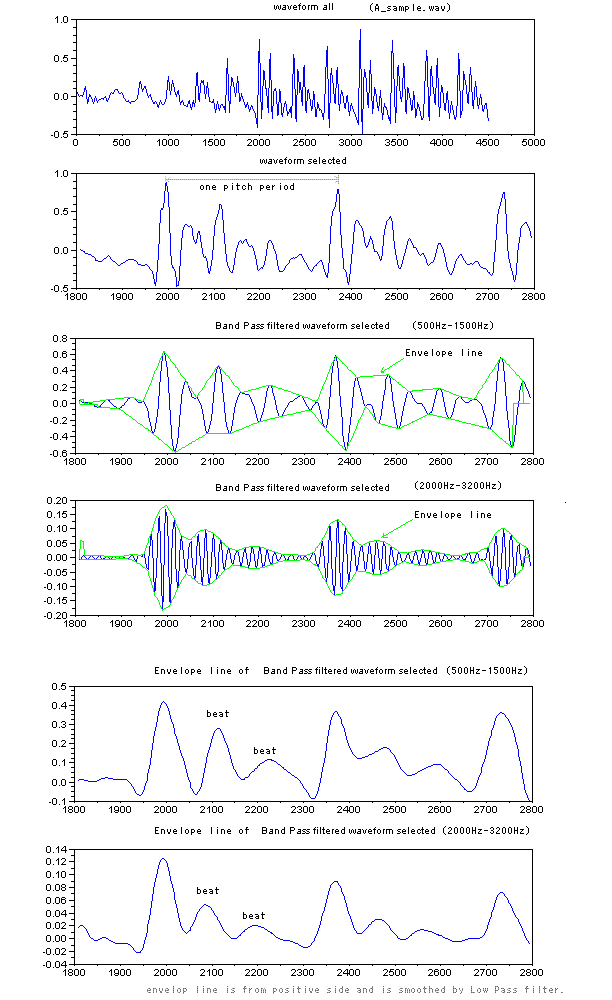
何十年前に比べれは、機械の信号処理能力は発達し、音声の信号を大量に確率論的に扱うことは得意？になった。確率データに構造を結びつけることによって、それが何であるかを裏付けできる認識マシーンができないであろうか？　

元の信号の分析解像度が同じならば、スペクトルを使おうとケプストラムを使おうと、それ以外を使おうと、本質的に分布群の構成は行き着くところは同じようになる可能性がある思う。

　子音は（発声器官の）特異な状態から母音状態への変遷過程であり、構造上の変移過程であり、構造上の運動が無駄な動きを避けることにより存在できる種類が特定されるのではないだろうか。つまり、分布上の変遷道筋も、構造不変に保つ変換が存在し、かつ、発声器官の特異な状態による種別から子音の数は有限の数に限られるのではないだろうか。

「分布に重なりがあると言うことは、まだ、未知の（識別するための）変数が隠されていると言うことだ。
識別関数の形式を工夫するのもよいが変数がわかればすっきり行くかもしれない。」

" Do not become a slave to such as trick-nology'."

No.3ｃ作成　2010年5月24日

むかしのホームページ

  音声信号の内部構造に基づく音声認識の研究

  「音声認識について考える」のエピローグ

   DFTと位相    SCILABを使って固有値と固有ベクトルを求める    ディエンファシス（de- emphasis）IIR フィルタ

   直線位相ＦＩＲフィルター     1次IIRフィルタの係数の推定    ヒルベルトの関係と最小位相    最小位相FIRフィルタ

   「音声の波形の生成を理解する」の目次音声波形のサンプル-日本語の５０音の単音の波形データの例

   確率論の手法と構造論との対比 FFT分析スペクトルと２管模型からのスペクトルの比較

   Chainerを使って 2次 IIR ノッチフィルターを学習できるか    FFTによるアップサンプリング(PYTHON)

   ディープラーニングと信号処理

No.136a（J版）作成　2015年9月23日

「この世での迷い迷走は　どの分野も同じ様なものだ。」

Thanks


Open Directory プロジェクトのミラー（2017年3月時点）	W3CによるHTMLの Web文法チェッカー

このWEBサイトを閲覧して頂きありがとうございました。

　　
since 2005.7.17

最終更新日2018年11月20日